285. La parte esencial de este instrumento consiste en un limbo circular vertical ZAP, fig. 71, que puede girar en derredor de la vertical CP, tirada por su centro, y que además puede hacerlo también verticalmente en derredor de un eje horizontal por este mismo centro tirado. Un anteojo OCL, provisto de un micrómetro de hilo fijo y de un nuñez, gira en derredor del centro C, y puede recorrer sucesivamente todos los puntos del limbo.
Para comprender su uso fijémosnos en la figura citada. Sea S un objeto remoto e inmóvil, cuya distancia zenit se desea medir. También será, si se quiere, una estrella. También será, si se quiere, una estrella. Porque, aunque los astros se disloquen a cada instante por efecto del movimiento diurno, pueden calcularse los efectos de esta alteración durante el intervalo de las observaciones, y tenerlos en cuenta, como dentro de poco se verá; lo que trae la cuestión al mismo estado que, si no hubieran de observarse más que puntos fijos. Supuesto esto, véase cómo se opera: comiénzase por fijar el nuñez del anteojo sobre el punto cero de la división; luego se dirige el limbo en el vertical del astro por medio del movimiento azimutal, y en seguida se le hace girar verticalmente en derredor de su centro, hasta que el puesto S corresponda al centro de los hilos; esto es lo que la fig. 71 representa. Concibamos ahora una plomada CP tirada por el centro del limbo; su dirección prolongada determinará el zenit Z, y el arco AZ leído sobre el limbo será la distancia del zenit. Pero se puede evitar el uso de este hilo y la lectura de este arco, del modo que va a verse.
286. Dispuestas las cosas como acabamos de decir, se comunica un movimiento al limbo azimutal en derredor de la vertical que pasa por su centro, y se le hace dar una media vuelta, de modo que se le traiga al vertical del astro (véase la fig. 72). En este movimiento no ha cambiado el punto Z del limbo. Sólo que si éste hacía primero cara al este, ahora la hace al oeste; y como el anteojo está fijo sobre el limbo, síguese que su dirección presente LAC forma siempre el mismo ángulo con la vertical. Entonces se desprende este anteojo, y haciéndole girar sobre el limbo, se le trae otra vez sobre el astro. Su nueva dirección CA´S corresponde entonces a otro punto del limbo, tal como A´; y una vez que se supone una inmóvil al astro, el arco A´Z es exactamente igual al arco AZ, o a la distancia al zenit. El arco total AA´, que el anteojo acaba de recorrer, es pues el doble de esta distancia. Así, leyendo este arco indicado por la dislocación del nuñez sobre la división del limbo, y tomando su mitad, se tendrá la distancia al zenit, sin que sea absolutamente necesario conocer el punto Z; y por consiguiente sin necesitar para nada de la plomada.
A la verdad, esto supone que el limbo, pasando de la primera observación a la segunda, ha girado exactamente en derredor de la vertical, de modo que cada uno de sus puntos se mantenga exactamente a la misma altura sobre el plano horizontal. Para asegurarse de esto se ata detrás del limbo y paralelamente a su plano un nivel de aire muy sensible que se ajusta, es decir, que se pone bien horizontal en la primera posición del círculo en que el limbo hacía, suponemos, cara al este; después, si el punto Z del limbo se ha dislocado algo por el retorno, cuando el limbo hace cara al oeste, lo advierte el nivel que se ha dislocado juntamente con él, y cuya burbuja no corresponde ya a los mismos puntos de la división del tubo. Entonces se restablece al limbo en la posición en que el nivel vuelve a entrar en sus primeros límites; y así, sin conocer el punto Z, se está siempre seguro de que vuelve a la misma vertical. Hay en todos los círculos tornillos de movimiento para hacer así trasportar el limbo por grados insensibles, y para ajustar el nivel.
287. Después que se tiene así a la distancia zenital doble, se obtiene la cuádrupla del siguiente modo: sin tocar al anteojo, se da vuelta al instrumento, y se coloca otra vez el limbo la cara al este, según estaba al principio. El anteojo toma entonces la dirección CA´L (fig. 73). Si se le llevase otra vez hacia el astro, permaneciendo fijo el limbo, volvería al punto A, desde donde ha partido, y se destruiría el arco que se le ha hecho recorrer. En vez de esto se le deja fijo en A´, pero se transporta el limbo haciéndole girar verticalmente en derredor de su centro hasta que el astro vuelva en el anteojo al centro de los hilos. Entonces el punto A´ está dirigido hacia el astro, y el punto de partida desciende a A, (fig. 74). Hecho esto, vuelve uno a hallarse en las mismas circunstancias en que se estaba al principio de la primera observación, (fig. 71), sólo que el punto de partida es A´, es decir, el fin del primer arco recorrido91. Partiendo de aquí, y operando del mismo modo, se puede hacer una nueva observación doble que traerá el anteojo a A´´; y como el arco A´A´ será igual a AA´, el total AA´A´´ será la cuádruple distancia al zenit, y dividiéndola por 4, se tendrá esta distancia simple.
Con la distancia cuádrupla puede tenerse la séxtupla por el mismo procedimiento; es menester volver el limbo de cara al este en su primera posición, y llevar de nuevo el punto A´´ hacia el astro sin soltar el anteojo. El nuevo punto de partida será entonces A´´; otra observación doble traerá el anteojo a A´´, y el arco AA´´A´´A´´ será el arco séxtuplo. Dividiéndole por 6, se tendrá el arco simple.
Continuando así indefinidamente, se obtendrá el múltiplo de la distancia que se quiera, y dividiendo el arco total recorrido por el número de observaciones, se tendrá la distancia zenital simple. Puede de este modo hacerse recorrer al anteojo muchas circunferencias totales que será preciso tener en cuenta. Empero, para ahorrarse el trabajo de contarlas una a una, basta leer una sola vez el arco doble, lo cual da a conocer la distancia simple; y cuando se han terminado las observaciones, se ve fácilmente el número de circunferencias enteras que hay necesidad de añadir para que el arco total, dividido por el número de observaciones, vuelva a dar la distancia simple, determinada aproximadamente por la primera lectura.
288. Examinemos ahora en qué consiste la ventaja de esta multiplicación. Ninguna tendría, si las divisiones hechas sobre el círculo fueran matemáticamente exactas, y si el observador dirigiese siempre bien la puntería; porque entonces una sola observación daría la distancia exacta al zenit. Mas como estas condiciones son imposibles de llenar en la práctica, suple a ellas por compensaciones la repetición de los ángulos.
En primer lugar, y por lo que hace al error de las divisiones, se ve que los arcos medidos se siguen sin interrupción sobre el limbo, de manera que el punto de este último, que es el fin de una observación, se convierte en origen de la siguiente. Esto hace que la suma de las observaciones, o el arco total recorrido no encierre absolutamente error alguno intermedio, sino solamente los dos errores de las lecturas extremas. Estos errores mismos se atenúan todavía, porque las alidadas del círculo llevan cuatro nuñeces que se leen separadamente, y cuyo término medio contribuye a marcar el principio y el fin del arco total con mayor probabilidad de exactitud. Por último, el leve error que aun puede resultar, no obstante estas precauciones, en las lecturas extremas, hallándose repartido por la división sobre el arco total recorrido sobre el limbo, no conserva ya más que una influencia insensible sobre el arco simple recorrido en una sola observación, a lo menos suponiendo a las observaciones suficientemente multiplicadas. Los errores de las divisiones se aminoran pues en el círculo repetidor por la repetición misma, y la compensación que entre ellos se verifica no es efecto de una probabilidad, sino de una certidumbre.
Mas hay otros errores que se destruyen por el principio de las probabilidades en el uso del círculo, y que quedan en los otros instrumentos. Tales son los errores de la puntería, que muy leves ya de suyo, se destruyen como los de nivel por su compensación fortuita en muchos millares de observaciones. Estos errores existen igualmente en las hechas con grandes instrumentos como el mural; pues el error de la puntería se reproduce en ellos, y el del nivel está representada por el error de la plomada. Mas el pequeño número de observaciones no permite esperar aquí una compensación tan exacta como en el círculo. Si se supone que la exactitud de los resultados medios esté en razón compuesta del número de observaciones, y de la longitud del radio del instrumento, cien observaciones hechas con un círculo de decímetros (7 I/2 pulgadas) de radio equivaldrán a una observación única hecha con un mural de 20 metros (24 varas). ¿Dónde podrían hallarse semejantes instrumentos, y sobre todo, cómo podría empleárselos en las observaciones que requieren viajes?
289. Después de haber explicado en general el mecanismo de la repetición y sus ventajas, se hace menester entrar en algunos pormenores sobre las comprobaciones particulares que deben hacerse con el instrumento antes de que se le emplee en las observaciones.
La primera condición que hay que llenar es que el limbo esté exactamente vertical, y pueda mantenerse en esta posición mientras se observa, o a lo menos, que se tengan medios de restablecerle en ella. Para esto se coloca detrás del limbo, y perpendicularmente a su plano, un pequeño nivel de aire que se sujeta al eje horizontal en torno del cual gira el círculo (fig. 75). Entonces, cuando el nivel es horizontal, el limbo es vertical por razón de la perpendicularidad. Ahora bien, hay en los círculos repetidores un tornillo de ajustar que hace mover el limbo y con el cual se le restituye a la verticalidad luego que el nivel perpendicular indica que se aparta de él.
Tocante a este nivel mismo, se ve que es horizontal cuando los extremos de la burbuja de aire que encierra terminan en dos rayas fijas, trazadas por el artista para este objeto. Pero es útil saber en caso necesario suplir a este dato.
Con efecto, aun suponiendo que este nivel hubiese sido perfectamente arreglado por el artista, pudiera suceder muy bien que se trastornase en su armazón y dejara de ser perpendicular al limbo. Ésta es la razón porque se lo comprueba antes de empezar las observaciones. Para esto se sujetan al limbo dos pinzas P y Q sobre las cuales se han trazado dos puntos sumamente finos que por construcción deben hallarse a iguales distancias del plano del limbo a que aquéllas están aplicadas. Los artistas tienen medios muy precisos y sencillos de llenar esta condición. En el uno de estos puntos, en el más elevado, se suspende una plomada y se hace mover el limbo hasta que esta plomada venga a dar exactamente sobre el otro punto. El limbo es entonces vertical, puesto que por construcción la línea de esta especie, tirada por los dos puntos P y Q, es paralela a su plano. Cuando se le ha traído a esta posición, se hacen mover los tornillos del nivel pequeño, de modo que se ponga exactamente horizontal, y las variaciones de este nivel indican luego si el limbo se aparta de la verticalidad. La delicadeza de este instrumento hace aun para esto preferible su uso al de la plomada, a la par que es incomparablemente más cómodo92.
Si se quisiere comprobar también las pinzas mismas sería muy fácil. Ajustado el pequeño nivel, es decir, vuelto horizontal, hágase girar el limbo verticalmente, en términos que la pinza que estaba arriba venga abajo y la de abajo arriba. Suspéndase entonces de nuevo la plomada; y si da todavía exactamente sobre los dos puntos P y Q, el limbo es vertical y las pinzas están bien arregladas. En el caso contrario la variación de la plomada será doble de la falta de paralelismo. Porque sea LL1, fig. 77, la dirección del limbo en su primera posición, haciendo con él cierto ángulo la vertical PQ por el error de las pinzas. En la inversión cada uno de los puntos P y Q describe un a circunferencia de círculo en derredor del eje de rotación ACC´, que es perpendicular al limbo. La línea PQ describe pues en derredor de este eje una superficie cónica cuyo ángulo en el centro es PC´P o Q´C´Q, designando P´ y Q´ las nuevas posiciones de los puntos P y Q después de la inversión. Si por el punto C´ se tira C´L´ paralela al limbo, esta línea, que se mantiene inmóvil durante la rotación, dividirá al ángulo Q´C´P en dos mitades, cada una de las cuales será igual al ángulo L´C´P, formado por la línea PQ con el limbo. Ahora, cuando se suspenda de nuevo la plomada en Q´, la cantidad Q´´Q´P´ en que se aparte de la línea P´Q´ será igual al ángulo en el centro Q´C´P; luego este apartamiento será doble del error del paralelismo.
Si se apercibiese un error de este género, sería menester ocuparse de corregirle. Para esto debe haber sobre las pinzas tornillos de movimiento que permitan alejar o aproximar los puntos P y Q. Se hará pues mover a estos puntos, en términos que se destruya la mitad del apartamiento observado, y con las pinzas así arregladas se volverá a poner vertical el limbo. Mas, como es muy difícil que se haga esta bisección desde la primera vez, cuando se haya restablecido con corta diferencia la verticalidad del limbo por medio de las pinzas corregidas, se aprovechará esta verticalidad aproximada para corregir nuevamente las pinzas, y procediendo así por una serie sucesiva de ensayos y correcciones, se llegará en breve a arreglarlo todo con exactitud. El pequeño nivel perpendicular al limbo indicará en seguida la conservación de la verticalidad; y aun se puede, repitiendo estas tentativas sobre diversos puntos del mismo, asegurarse de que el eje de rotación le es exactamente perpendicular; porque, si no lo fuera, las posiciones de la plomada no concordarían entre sí sobre los diferentes radios del círculo.
290. En rigor, podrían satisfacer estas precauciones relativamente a la verticalidad, porque si se la hallase alterada en una observación, los tornillos de movimiento del instrumento bastarían para restablecerla en virtud de la indicación del nivel perpendicular. Pero como esta operación invierte siempre algún tiempo, es preciso hacerla tan rara como se pueda. Fuerza sería sin embargo efectuarlo a cada observación por el retorno del círculo, si la columna que le conduce no fuera exactamente vertical. Porque si en la primera posición del instrumento cuando hace frente al este, LM (fig. 78) fuera el limbo supuesto vertical, y AB la columna inclinada al horizonte: como ésta se mantiene inmóvil en el retorno, el limbo tomaría, pasando al oeste, la dirección L´M´, siempre igualmente inclinada sobre este eje, pero no ya vertical; de modo que sería preciso restituirle la verticalidad, y restituírsela así sucesivamente, al pasar de un lado a otro en cada observación.
Se evitan estos inconvenientes haciendo vertical a la columna, y se la trae a este estado por medio de tres tornillos que lleva el círculo horizontal sobre el cual se levanta esta última y que sirve de base a todo el instrumento. Estos tres tornillos, designados por V,V´,V´´ en la fig. 79 están espaciados por intervalos iguales, de manera que los radios CV,CV´,CV´´ tirados perpendicularmente al eje de la columna, hagan entre sí ángulos iguales al tercio de la circunferencia. El procedimiento consiste en hacer primeramente horizontal a uno de estos radios, por ejemplo, a CV, y en hacer después girar al plano VV´V´´ en torno de esta línea como eje, en términos que se le haga por último perfectamente horizontal en todos sentidos. Entonces el eje CC´, que por construcción es perpendicular a este plano, se halla necesariamente vertical.
Para esto, se aprovecha el gran nivel NN´, que está adaptado a la columna del círculo, y sirve para conservar el zenit en los retornos. Se dirige el limbo por el vertical del tornillo V, y se pone horizontal al nivel; en seguida se comunica al círculo un movimiento azimutal en derredor de la columna CC´, y se le hace dar una media vuelta que trae de nuevo al limbo al vertical del tornillo V. Pero entonces los dos extremos del nivel han cambiado de posición relativamente a este tornillo. Aquel que era sur se ha vuelto norte, y recíprocamente. Toda vez que la rotación se ha hecho en derredor de la columna CC´, el nivel ha descripto una superficie cónica en derredor de esta línea como eje. Si este eje es vertical, dicha superficie se convierte en un plano horizontal, y el nivel no está trastornado. Mas si la columna se halla inclinada al horizonte, el nivel no puede ser ya horizontal, y la inclinación que su desvío produce se dobla por el retorno. Corrígese pues la mitad de esta variación haciendo marchar al tornillo V en el sentido conveniente, es decir, levantando o bajando el punto V según la indicación del nivel. Después se acaba la otra mitad de la corrección haciendo marchar al nivel mismo por sus tornillos de movimiento, hasta que se encuentre así restituido al punto de igualdad en que primero se le había colocado. Empero, como nunca hay seguridad de haber hecho la bisección con exactitud, se vuelve a empezar la operación con el nivel corregido de este modo. Si el retorno da todavía una diferencia, ésta es incomparablemente menor, y en pocos ensayos se llega por último a destruirla.
Entonces la columna CC´ se halla traída a un plano vertical, perpendicular a la dirección del radio CV. Mas esto no basta todavía para que esta columna sea vertical, porque puede aun ladearse hacia V´ o hacia V´´; así que dirigiendo el limbo por cada uno de estos azimús se encuentra siempre que se desvía en sentidos opuestos, y en una cantidad igual. Por lo que, levantando uno de los tornillos y bajando el otro en cantidades iguales, se debe restablecer la verticalidad, y hallar el nivel exacto en todos sentidos, sin que sea necesario tocar a él; y esto es con efecto lo que sucede. Pero, como no se opera nunca esta división de una manera muy exacta, síguese que el primer radio CV no conserva enteramente su horizontalidad después de estas operaciones. Se vuelve pues a empezar de nuevo a restablecer la verticalidad del eje, partiendo de este radio. Esta vez sin embargo las correcciones son incomparablemente menores, y con un poco de costumbre se consigue hacer vertical al eje después de dos o tres ensayos. Entonces el nivel se conserva horizontal, cualquiera que sea el azimut por que se dirija el limbo. La operación que acabamos de describir se verifica ordinariamente antes de las demás comprobaciones, porque nunca son éstas tan fáciles como cuando el eje es vertical.
291. Cuando se han hecho todas estas comprobaciones, si se sujetan las pinzas al limbo y se suspende sobre ellas la plomada, deberá dar sobre los dos puntos de señal P y Q, cualquiera que sea el azimut en que se le sitúe, y al mismo tiempo el gran nivel paralelo y el pequeño perpendicular al limbo deben conservar su horizontalidad sin ninguna alteración. Esta última prueba abraza y confirma todas las otras.
292. Sólo falta ya que arreglar el eje óptico del anteojo. Hácese esto por medio del anteojo de prueba, según se ha explicado para el mural en el tomo I, § 183. Si no se tuviese anteojo de prueba, podría suplírsele por medio del círculo azimutal que sirve de base de la columna y está ordinariamente dividido como el círculo vertical. Véase en lo que consiste este procedimiento. Diríjase el anteojo sobre un punto muy lejano y situado en el horizonte o muy cerca de él; para esto no es de consecuencia una discrepancia de diez o doce grados. Léase sobre el círculo azimutal el número de grados y minutos a que corresponde el índice de la columna; o para mayor exactitud, escójase el punto de mira de modo que este índice corresponda a una división exacta, en términos que pueda responderse de su posición poco más o menos. Leído bien que sea el azimut, hágase girar la columna una semicircunferencia, de modo que el índice que correspondía primeramente al azimut A, corresponda ahora al azimut A + 200g, y después de haberle situado con mucha exactitud en esta posición, fíjesele de una manera invariable por medio de su tornillo de presión. Por esta operación ha dado una vuelta el anteojo; suéltesele, y haciéndole escurrir sobre el limbo, tráigasela otra vez al punto de mira, cabalmente como si se quisiera tomar su distancia al zenit en una observación par. Si el eje óptico del anteojo es paralelo al plano del limbo, se debe volver a hallar el punto de mira en la intersección de los hilos. Empero si este eje tiene la más leve inclinación, como en el retorno describe una superficie cónica en derredor del eje central perpendicular al limbo, el punto de mira no podrá ya volver a hallarse en la intersección indicada, y se apartará de ella a derecha o izquierda. Si el eje óptico se acerca realmente al limbo por el lado del objetivo, el punto de mira parecerá alejarse. Por el contrario, si esta extremidad del eje óptico se aleja del limbo, el punto de mira parecerá acercarse, porque los anteojos invierten; y como el plano del limbo se halla siempre en el mismo vertical, el apartamiento aparente del punto de mira es doble del error ocasionado por la inclinación del eje óptico. Esto es lo que muestra la fig. 80 en que ACB representa el plano vertical del limbo, L´CO´ la primera dirección del anteojo hacia el objeto O´, que corresponde al centro de los hilos, L´´CO´´ la dirección del anteojo al cabo del retorno, y O´O´´ el desvío del objeto O´ por efecto de la inclinación del eje óptico sobre el plano del limbo, desvío doble de O´B que representa el efecto real de esta inclinación.
¿Quiérese medir este error? Pues suéltese el índice del círculo azimutal, de modo que pueda hacerse girar la columna, y tráigase en seguida otra vez la intersección de los hilos sobre el punto de mira; el ángulo recorrido por el índice sobre el círculo azimutal será igual al ángulo O´´CO´, y por lo tanto doble del error O´´CB, suponiendo que el objeto esté en el horizonte. Si esta última condición no estuviese satisfecha, el ángulo recorrido sobre el círculo azimutal será la proyección real del ángulo verdadero. Si hemos escogido el objeto en el horizonte, es a fin de que la operación diese desde luego esta medida.
Mas en vez de medir el error ¿se quiere corregirle? No hay más que restituir los hilos del micrómetro al punto de mira, y hacerlos así marchar hasta que se haya destruido la mitad del desvío. Si se ha hecho con exactitud esta bisección, el eje óptico se habrá hecho paralelo al plano del limbo. Pero como nunca hay seguridad de verificarla por la primera vez, se empieza de nuevo la comprobación con este eje óptico arreglado ya, y en pocas pruebas se llega a alcanzar el paralelismo con todo el grado de exactitud necesaria; grado que el cálculo determina, como se verá por las notas que ponernos aquí93.
Por medio de las comprobaciones que acabamos de describir, el círculo se arregla completamente, y se puede hacer desde luego uso de él para las observaciones. Todas ellas son más largas de explicar que de hacer, cuando se está acostumbrado al manejo del instrumento.
293. Réstanos ahora explicar como, cuando se observan las alturas de los astros con el círculo repetidor, se pueden eludir los efectos del movimiento diurno, y operar absolutamente como si el astro fuera inmóvil.
En primer lugar, al hacer estas observaciones, no se puede ordinariamente tener más que dos objetos: hallar la hora por medio de la altura observada, o hallarla altura meridiana del astro. Examinemos sucesivamente estos dos casos.
Para tener la hora es preciso determinar el ángulo horario por medio de la altura observada. Es pues ventajoso observar lejos del meridiano, porque entonces las alturas de los astros varían con mayor rapidez; al paso que, acercándose al meridiano, llegan a ser casi constantes, y una levísima variación en aquélla corresponde a una gran diferencia de ángulo horario; de modo que un error muy pequeño en la observación de la altura, introduciría otro de consideración en el tiempo absoluto. El cálculo hace ver que el movimiento en altura es el más rápido cuando el azimut es de 100g. Entonces el astro se halla en el plano vertical que contiene a los puntos de este y oeste, y el cual se llama ordinariamente el primer vertical. Ésta es particularmente la posición en que es ventajoso observar las distancias al zenit para inferir de aquí el tiempo. Mas todos los astros no pueden satisfacer a esta condición: porque hay muchos entre ellos que no pasan por el primer vertical. Felizmente esta condición no es tampoco rigurosamente necesaria, y cuando las circunstancias no permiten someterse a ella, lo que ocurre con mucha frecuencia, es preciso únicamente escoger el instante de la observación y la altura del astro, de manera que las variaciones de esta última sean bastante rápidas para que no se aumenten considerablemente los errores inevitables de las observaciones cuando se deduce de ellas el ángulo horario. Es siempre fácil determinar para cada astro los convenientes límites, calculando anticipadamente los pequeños cambios de ángulo horario que corresponden a levísimas variaciones de altura. En general, se comprende que se hará preciso, en cuanto sea posible, elegir estrellas situadas cerca del ecuador, a fin de que tenga más rapidez su movimiento diurno, y evitar las estrellas circumpolares cuyo movimiento es demasiado lento94.
294. Supongamos, pues, que se hayan tomado estas diferentes precauciones: se observan las distancias del astro al zenit, como se haría si estuviese fijo; pero a cada observación sea par, sea impar, se anota exactamente la línea, el minuto, el segundo y la fracción de segundo a que el astro se ha situado en el centro de los hilos. Cada par de observaciones requiere a lo menos dos minutos, algunas veces uno solo, según la habilidad del observador. De vez en cuando, y al final de una observación par, se lee sobre el limbo el arco recorrido.
295. Cuando se hace la lectura de los arcos, al cabo de cada par de observaciones, supuesto que sea su intervalo de dos minutos sexagesimales, se echa de ver que en el de ocho o diez minutos las alturas observadas crecen proporcionalmente al tiempo, de modo que el valor medio de ellas corresponde exactamente a la época media, a lo menos cuando se observa bastante lejos del meridiano según hemos indicado. Bien probado esto, se excusa leer los arcos al final de cada observación par, lo que envuelve dilaciones. Se leen al cabo de seis u ocho observaciones; en una palabra, después de un número de pares que comprendan ocho o diez minutos de tiempo: llámase a este conjunto una serie, y se hace corresponder la época media de las observaciones con el arco medio recorrido sobre el limbo. Empero, si se prolongase más tiempo una misma serie, o si se observase muy cerca del meridiano, este método sería inexacto, como la experiencia y el cálculo concuerdan igualmente en probarlo95.
296. Teniendo así la distancia media del astro al zenit y la época media que le corresponde en tiempo del péndulo, se resolverá con esta distancia el triángulo esférico que da el ángulo horario. Reducido este ángulo a tiempo sideral, dará el número de horas, minutos y segundos siderales comprendidos entre la época de las observaciones y el paso del astro por el meridiano. Si en este cálculo se tiene cuidado de contar los ángulos horarios a empezar desde el meridiano superior y en el sentido del movimiento diurno, desde 0 hasta la circunferencia entera, bastará añadir el ángulo horario calculado a la ascensión recta del astro reducida a tiempo, y la suma será el ángulo horario del punto g del ecuador o la hora sideral, § 18. Entiéndese que antes de emplear la distancia zenital observada para calcular el ángulo horario es preciso corregirla de la refracción. En cuanto a la distancia polar del astro, que es también uno de los elementos de este cálculo, se la toma en los catálogos astronómicos, por ejemplo, en el Conocimiento de los Tiempos; pero como estos catálogos sólo dan la posición media del astro, se hacen en ellos las pequeñas correcciones relativas a la precesión, nutación y aberración para convertirla en posición aparente.
297. Si el astro observado es el Sol, el ángulo horario observado así, y contado desde medio día o media noche, dará la hora solar. Los astrónomos franceses, conformándose con el uso generalmente establecido en la sociedad, cuentan estas horas a empezar desde el meridiano inferior o desde media noche, y van de este modo desde 0 a 24 horas sexagesimales, o desde 0 a 10 horas decimales, según que emplean la división sexagesimal o decimal del tiempo.
Como el disco del Sol tiene un diámetro sensible, no se puede en las observaciones consecutivas abarcar su centro como con una estrella, y situarle bajo el hilo. Elúdese la dificultad poniendo una vez el hilo sobre el borde superior y otra sobre el inferior. Por este medio una de las distancias es demasiado pequeña en todo el semidiámetro del disco; pero la siguiente es demasiado grande en la misma cantidad; y como las observaciones con el círculo repetidor se hacen siempre en número par, síguese que se efectúa siempre en cada serie una compensación exacta. Igual artificio se emplearía, si se observase a un planeta o aun a la Luna. Casi es inútil recordar que para observar al Sol se pone delante del ocular un vidrio ennegrecido, y que para observar a los demás astros por la noche, es preciso iluminar los hilos del micrómetro, a excepción de la Luna, cuyo resplandor basta para el efecto.
298. Cuando se observan estrellas, es muchas veces difícil y aun imposible ponerlas exactamente en el centro de los hilos, como debería hacerse, para que sus imágenes se hallasen precisamente en el eje óptico del anteojo. Procede la dificultad de que los hilos se cruzan en este centro, lo que aumenta su espesor, hablando más exactamente, el lugar que ocupa su imagen en el campo del anteojo. Entonces, cuando se pone a la estrella detrás del centro de los hilos, sucede que se halla toda oculta, y no podría responderse de volverla a poner siempre con igual exactitud en el punto mismo detrás de los hilos. Este inconveniente se evita no observando en el cruzado mismo de los hilos, sino a una distancia muy pequeña, sobre el hilo horizontal. Mas, como a pesar de todo el esmero del artista es imposible que este hilo no tenga alguna leve inclinación, se trata de eludir este efecto observando siempre en el mismo punto del hilo, o a lo menos en puntos muy poco distantes. Para esto, si en la primera observación y suponiendo el anteojo a la derecha del observador, se ha puesto la estrella algo a la derecha del centro de los hilos, lo que la sitúa en realidad un tanto demasiado cerca del limbo, una vez que nuestros anteojos invierten los objetos, se la coloca en seguida algo a la izquierda de este centro en la segunda observación en que el anteojo está a la izquierda, lo que en realidad la pone demasiado cerca del limbo, como la primera vez. Hállase entonces que se ha referido siempre el astro al mismo punto físico del hilo, o a una distancia tan corta, que el efecto de la inclinación de este último en tan breve intervalo apenas tiene influencia sobre la altura observada. A la verdad, apártase uno algunos segundos a derecha o izquierda del eje óptico; pero el error es enteramente insensible, como puede probarse por las fórmulas que hemos dado anteriormente, § 279, (nota), para medir este error.
299. El método que acabamos de exponer es el de las alturas absolutas. No era practicable el mismo con los antiguos cuartos de círculo que, a causa de los errores de división que los afectaban casi siempre, no daban las distancias al zenit con bastante exactitud. Recurríase, pues, más ordinariamente al método de las alturas correspondientes que explicamos en el § 173 del tomo I. Ahora el de las alturas absolutas es el más exacto de todos, gracias a la invención del círculo repetidor que permite medir estas alturas con la última precisión. Pueden aumentarse todavía sus ventajas observando muchas series de un mismo astro y tomándolas de una y otra parte del meridiano, lo cual evita todos los errores de ascensión recta y aun atenúa los de la refracción. Con todas estas precauciones nos atrevemos a afirmar que el círculo repetidor ofrece el medio más seguro de determinar el tiempo, sea absoluto, sea relativo, y no dudamos de que bajo este concepto sobrepuja al mismo anteojo meridiano.
Para completar estas nociones, hemos puesto en nota ejemplos de cálculos de tiempo absoluto por las alturas de una estrella y del Sol. Es indispensable la práctica de este procedimiento, porque la determinación del tiempo forma la base de todo cálculo astronómico, y los medios de obtenerle con rigor son tan fáciles, que no tendría disculpa el dejar de emplearlos en las ocasiones en que esto llegue a ser necesario96.
300. El otro género de observaciones que puede hacerse con el círculo repetidor es la medida de la altura meridiana de los astros. Para ello, pocos momentos antes de que el astro pase por el meridiano, se empieza una serie de distancias al zenit que se continúa hasta después del paso, a una poco más o menos igual. La distancia media, dada por esta serie, discrepa poco de la distancia meridiana. No le es, sin embargo, enteramente igual; toda vez que ésta en los pasos superiores es la menor, y en los inferiores la mayor de cuantas puedan observarse. Empero, señalando con exactitud la hora, minuto, segundo y fracción de segundo en que se ha hecho cada observación particular, y conociendo por otra parte la época precisa del paso del astro por el meridiano y su distancia polar, se sabe calcular la corrección de que ha menester cada distancia. Esta corrección no es ya simplemente proporcional a las variaciones del ángulo horario como en las alturas observadas lejos del meridiano; lo es al cuadrado del seno de la mitad de este ángulo. En los pasos superiores es sustractiva de las distancias al zenit porque entonces la distancia meridiana es la menor de todas; en los inferiores es aditiva por una razón opuesta97. Como el arco recorrido sobre el limbo es igual a la suma de todas las distancias observadas, se le aplica la de todas las correcciones en el sentido conveniente, y se tiene tantas veces la distancia media como observaciones en la serie; de forma que para hallar esta distancia basta dividir la suma de los arcos y de las correcciones Por su número lo que viene a ser lo mismo, se toma el término medio de las distancias observadas, se le aplica el término medio de todas las correcciones, y se tiene la distancia meridiana tal como se la habría observado inmediatamente. El complemento de esta distancia es la altura meridiana.
301. Parece que este procedimiento implica un círculo vicioso. Porque, a fin de calcular las correcciones de que acabamos de hablar, es preciso conocer ya la distancia polar del astro, su distancia meridiana Z y la distancia D del polo al zenit. Y precisamente es para hallar una de estas cosas para lo que se hacen las observaciones de que hablamos aquí. Empero, nótese que el conocimiento exacto de estos elementos no es de modo alguno necesario; basta su valor, aunque sea nada más que groseramente aproximado. Porque los errores que en él pueden cometerse se atenúan considerablemente, mediante a que en la expresión de la reducción al meridiano se hallan multiplicados por el cuadrado del seno de la mitad del ángulo horario, cantidad que es siempre una fracción sumamente pequeña mientras no se aparte uno mucho del meridiano. De modo que el influjo de estos errores sobre el valor de la reducción, que llamaremos d, se hace enteramente insensible. Ésta es la razón por lo que, si es conocido el astro observado, bastará tomar su distancia polar en el Conocimiento de los Tiempos o en las cartas celestes. Y si además se conoce poco más o menos la latitud, o bien la distancia D del polo al zenit, se sacará un valor de Z, es decir, de la distancia meridiana, suficientemente aproximado para calcular la pequeña reducción d. Mas si la latitud no es conocida ni aun aproximadamente, no hay sino emplear primeramente para Z la distancia media observada sin otra corrección que la de la refracción; y con este valor y el de la distancia polar @, que se supone conocida, se calculará a D o sea la distancia del polo al zenit. Por medio de estos valores aproximados se obtendrán los de d o las correcciones que hayan de hacerse a las observaciones para tener su verdadera distancia meridiana; y reproduciendo el cálculo con esta distancia corregida se sacará un valor más exacto de D. Entonces estos elementos serán conocidos con bastante precisión para poderlos emplear en el cálculo definitivo de la reducción al meridiano.
A la verdad, aun tomamos en tal caso de las Tablas la distancia polar del astro. Estas distancias son conocidas con la mayor precisión en el presente estado de la Astronomía para las principales estrellas. Mas si el astro observado fuera desconocido, sería necesario suponer por lo menos que se conocía la latitud del lugar en que se observaba, y por consiguiente la distancia del polo al zenit. Entonces, con esta distancia y el valor observado de Z se calcularía aproximadamente el de @, lo que bastaría para tener las correcciones d, y por consiguiente a Z y @ con más exactitud por medio de un segundo cálculo como en el caso anterior.
Por último, si se quisiera que el observador lo sacase todo de sus propias observaciones, sería menester ante todo que determinase aproximadamente la latitud por los pasos superiores e inferiores de las estrellas circumpolares, lo que no requiere el conocimiento de la distancia polar, y luego se ocuparía de los otros astros. Tal es la marcha de invención que hemos seguido en los anteriores capítulos; pero es preciso aprovecharse en la aplicación de todo lo que ya es conocido.
302. Hemos supuesto que los ángulos horarios correspondientes a cada observación son dados en tiempo por el reloj. Para esto sería preciso que éste siguiese exactamente el tiempo sideral, si es una estrella la que se observa; o el tiempo solar si es el Sol, o en general, que su marcha fuera conforme con la del astro observado. Es casi imposible llenar rigorosamente esta condición, pero no es indispensable; hasta que el movimiento de reloj sea bien conocido y se le reduce a lo que debería ser por medio del cálculo. Si este movimiento se aparta poco de la marcha del astro, entonces sólo resulta una leve corrección que hacer en el resultado definitivo98.
Es casi inútil añadir que, si el astro observado tiene un diámetro sensible, se hace preciso poner alternativamente en contacto el hilo con su borde superior e inferior. Empero, y esto es mucho más importante de advertir, si el astro tuviese un movimiento en declinación, habría necesidad de tomarle en cuenta; porque la distancia meridiana que se deduce de cada observación parcial por medio de las reducciones anteriores es la que tendría realmente lugar, si la declinación del astro se conservase siempre la misma que en la época de observación. Si esta declinación varía, la distancia reducida debe discrepar de la distancia meridiana verdadera, y la diferencia ser igual al cambio de la declinación desde la época de la observación hasta el paso por el meridiano. Ésta es la razón porque, si se supone uniforme al movimiento en declinación durante la duración entera de la serie, será preciso calcular proporcionalmente la corrección de cada distancia reducida en razón del ángulo horario que a ella corresponde. Estas correcciones serán patentemente de signo contrario antes y después del paso por el meridiano, suponiendo, como es el caso ordinario, que el cambio de la declinación se prosigue en el mismo sentido durante toda la serie: porque entonces, si este cambio aumenta las distancias al zenit en un lado del meridiano, las disminuirá en el otro. De aquí resulta esta regla muy sencilla: Hágase separadamente la suma de los ángulos horarios observados antes y después del paso, expresados que sean estos ángulos en tiempo, por ejemplo, en minutos. Réstense estas dos sumas una de otra, divídase su diferencia por el primero de observaciones, y multípliquese el resultado por el movimiento del astro en declinación para un minuto de tiempo, movimiento que es dado por las tablas astronómicas. El producto será la corrección que es preciso aplicar a la distancia meridiana, calculada en virtud de la totalidad de la serie, como si la distancia polar fuese constante.
303. Una sola serie de esta clase, hecha para un astro cuya distancia polar meridiana se conoce, basta para determinar la latitud del lugar en que se observa, porque si el astro pasa por el meridiano, como en la figura 81, restando su distancia meridiana ZS de su distancia polar PS, se tendrá la distancia PZ del polo al zenit. Si por el contrario, el astro pasa por el meridiano del lado del polo, como en la fig. 82, se añadirá en los pasos superiores la distancia polar a la meridiana, y se la restará en los inferiores. De todos modos se tendrá la distancia del polo al zenit, y por consiguiente la latitud que es su complemento. Entre las estrellas que pueden escogerse para determinar así la latitud, la polar es la preferible, porque es aquella para la cual son más pequeñas las reducciones al meridiano. Esto depende de lo corto de su distancia al polo99.
Ella es también la que se ha observado más en estos últimos tiempos; por consiguiente, es perfectamente conocida su distancia polar. Puédese aun emplear con seguridad a de la osa menor, que se ha observado también mucho por Mechain y Delambre.
304. Cuando se quiere determinar con suma precisión una latitud, por ejemplo, para la medida de una meridiana, o para el trazado de una gran carta, se procura hacerlo independientemente de la misma distancia polar. Para esto se observan con el círculo repetidor los dos pasos superiores e inferiores de una misma estrella circumpolar, por ejemplo, de la polar misma, o de la de la Osa menor. Se reducen estas observaciones al meridiano con los valores de la distancia polar más exactos que puedan proporcionarse, y de cada una de ellas se saca una distancia del polo al zenit, afectada de todo el error que pueda haberse cometido en la distancia polar. Empero este error influye en sentido contrario sobre los resultados de los dos pasos. Desaparece pues en su suma, que da así la distancia del polo al zenit, y se duplica en su diferencia que da el error de la distancia polar. Esta compensación es enteramente parecida a la que se hace en las distancias meridianas del Sol cuando se observan los dos bordes100.
Por este procedimiento, así como cuidando de observar la más escrupulosa exactitud, es como se ha determinado la latitud de París, y la de muchos puntos situados sobre el arco de meridiano, comprendido entre los paralelos de Formentera y Dunkerque: así es pues como se han hecho las observaciones de Mechain y Delambre de que se ha hablado en el estado del § 198 del tomo I.
La determinación de la figura de la Tierra ha sido de siglo y medio a esta parte uno de los más constantes objetos de los trabajos de la Academia de ciencias de París. Desde la primera medida del grado verificada por Picard, la cual sirvió a Newton para comprobar la existencia de la gravitación universal, se han empleado los esfuerzos de la astronomía más delicada, las de la física más escrupulosa y los de la más profunda geometría para fijar los elementos de este gran fenómeno y desenvolver las consecuencias que podían suministrar, no sólo sobre la forma, sino también sobre la constitución interior del esferoide terrestre. Hanse aplicado tres métodos, o más bien tres clases de pruebas diferentes a esta investigación. El primero, directo y puramente gráfico, consiste en medir arcos de meridianos y paralelos sobre diferentes puntos de la superficie, es decir, en determinar por la observación las longitudes de estos arcos, sus amplitudes astronómicas, sus inflexiones y los ángulos bajo los cuales se cortan: y luego, en construir geométricamente la configuración del esferoide sobre el cual deben colocarse. Aplicada esta construcción a los resultados de todas las operaciones modernas, da indudablemente a la Tierra una forma aplanada en los polos, elevada en el ecuador, de conformidad con lo que la analogía indica para el equilibrio de una masa fluida que gira en derredor de un eje, y cuyas partes todas se atraen mutuamente. Pero cuando se quiere ir más allá de esta primera indicación, y asimilar el esferoide a una forma sencilla, por ejemplo al elipsoide, descúbrense en él irregularidades muy sensibles que le apartan de ella, y cuya irregularidad es incontestable, porque exceden en mucho a los errores que pudieran atribuirse a las observaciones. Cuando se examina, por ejemplo, de este modo el arco de meridiano que se extiende desde Greenwich a Formentera, las partes sucesivas de este arco, consideradas yendo del norte al sur, dan decrementos de grados que carecen absolutamente de toda ley, y presentan una grandísima anomalía hacia el 46º en particular. El arco en paralelo, medido recientemente entre Burdeos y Padua, ofrece fenómenos análogos, porque, reducidas sus diversas partes a una misma latitud, ofrecen en la extensión de los grados consecutivos, diferencias considerables semejantemente desprovistas de toda ley. Irregularidades análogas, no menos grandes que ciertas, se manifiestan también sobre las diferentes partes del arco meridiano medido por los ingleses en la India; y los señores Plana y Carlini las han hallado aun mayores en el Piamonte. Estos ejemplos demuestran que la figura de la Tierra es mucho más complicada de lo que se había creído en principio; y he aquí por qué se ha procurado atenuar la influencia de sus irregularidades combinando los valores medios de los grados medidos a latitudes muy distantes, y sometiéndolos a las relaciones elípticas, a fin de deducir el achatamiento del esferoide según ha podido verse en el capítulo XVII, sección IV del presente tomo. Mas en virtud de lo que acabamos de decir, es evidente que este resultado no pasa de una aproximación, cuya exactitud sería difícil apreciar, y que en todo caso no podría tener una aplicación física rigorosa.
Otro método de determinar el achatamiento del esferoide es aquel que se infiere del influjo que ejerce sobre los movimientos de la Luna. Este procedimiento se debe a Laplace. Supone que el esferoide discrepa poco de una esfera, lo cual, relativamente la Tierra, es un hecho incontestable. Cualquiera que sea la constitución interior de un esferoide semejante, su atracción sobre un punto exterior puede expresarse por una serie cuyos términos están ordenados según las potencias inversas de la distancia. El primero de estos términos representa la atracción de una esfera igual, en masa al esferoide; el segundo, lo que se añadiría a esta atracción, si el esferoide fuese elíptico; por último, los siguientes, expresan del mismo modo lo que es menester añadir a los primeros para completar los efectos de la verdadera figura. Ahora bien, hallándose divididos estos primeros términos por menores potencias de la distancia, son los solos que sensibles cuando se calcula la acción de la Tierra a una distancia tan grande como aquella a que está la Luna colocada; y por consiguiente, cuando se consigue poner en claro en los movimientos de este satélite las desigualdades de que son causa, puédese en virtud de tales efectos estimar el valor respectivo de los términos que los han producido. Obtendríase pues el valor verdadero del achatamiento, si el esferoide fuera exactamente elíptico; y cuando no lo sea, se obtiene lo que pudiera llamarse la parte elíptica del achatamiento. Laplace encuentra así para la Tierra 1/304 de achatamiento, según las observaciones de Burg; y este resultado discrepa apenas de aquel que da la comparación de los grados medidos en latitudes muy distantes. Semejante concordancia, si estuviese fundada sobre relaciones rigorosas, probaría que el esferoide terrestre era puramente elíptico; pero pierde mucho de su fuerza esta consideración, cuando se considera la extensión de las irregularidades que es menester despreciar en los arcos parciales del mismo meridiano, así como las suposiciones que es indispensable admitir por deducir por este medio el achatamiento.
El tercero y último método para determinar la figura de la Tierra se funda en la observación de las variaciones de la pesadez en las diferentes latitudes apreciadas por las observaciones del péndulo.
Según lo que se ha manifestado en los §§ 237 y siguientes, la hipótesis de la elipticidad de la Tierra envuelve como consecuencia lógica y necesaria que las intensidades de la pesadez absoluta de los cuerpos en los diferentes puntos de aquélla vaya creciendo proporcionalmente al cuadrado del seno de la latitud, yendo del ecuador hacia los polos, o lo que es igual, que las longitudes del péndulo de segundos que respectivamente la determinan crezcan del mismo modo en igual dirección. La recíproca de este hecho sería igualmente verdadera. Por consiguiente, siempre que se demostrase por la observación que las longitudes del péndulo que diese igual número de oscilaciones durante un segundo de tiempo en los diversos lugares de la superficie terrestre, o lo que es lo mismo que las intensidades de la pesadez de que en ellos estaban animados los cuerpos, variaban en proporción al cuadrado del seno de la latitud acercándose a los polos, tendríamos aquí un indicio de que la figura de la Tierra era un esferoide achatado hacia los últimos y elevado hacia el ecuador. Y conocida que fuese igualmente por la observación la longitud de este péndulo, podríase determinar siguiendo la misma marcha inversa el achatamiento de este esferoide.
Efectivamente, se sabe por la teoría del péndulo que llamando 2g a la fuerza de la pesadez, representada por el doble del espacio que describen los cuerpos durante el primer segundo de su descenso vertical, l a la longitud del péndulo de segundos tomado por unidad y p, al número 3,1415926, que 2g = l p2. Esto permite sacar el valor de esta pesadez, conocida que sea la longitud l. Así es como habiéndose determinado en el observatorio de París por experiencias muy delicadas que esta longitud era de 0m,99384, se ha sacado 2g = 9m,8088 para dicho lugar.
Esto supuesto, siendo dos las causas que contribuyen a modificar la intensidad de la pesadez en los diferentes puntos de la Tierra, y hacerla, como lo es, variable y creciente desde el ecuador a los polos en la hipótesis elíptica, una la desigualdad de acción de la fuerza atractiva y otra el influjo de la fuerza centrífuga, es claro que, si se conoce a una de ellas, a la última por ejemplo, al mismo tiempo que se determina por la experiencia la pesadez tal como la observamos modificada por ambas, sería posible entonces inquirir la influencia de la primera; y como ésta se halla ligada en último resultado a la diferencia de los dos ejes, el péndulo puede en su consecuencia ofrecer el medio de averiguar tal diferencia, o sea el achatamiento mismo de la Tierra.
Según un gran número de observaciones hechas con el péndulo de segundos bajo todas las latitudes accesibles al hombre, la diferencia total de la pesadez en el ecuador y en el polo es 1/194 de la pesadez en este último; y como la cantidad en que la fuerza centrífuga disminuye la pesadez en el ecuador es sólo 1/289, la diferencia de estas dos fracciones, o 1/590, es la disminución de la pesadez debida al achatamiento de la Tierra, lo que da 1/320 para este achatamiento mismo. Otros, siguiendo el mismo procedimiento, le valúan en 1/298,2, y no falta quien le haga subir a 1/282.
Los valores del achatamiento, calculados por este método, ofrecen grandes diferencias por las anomalías que presentan las variaciones de la longitud del péndulo de segundos a diversas latitudes que, aunque menos influidas en general que las de los grados de meridiano por las causas perturbadoras de la regularidad de la Tierra, se alteran por otras locales cuya energía llega a veces a hacerse bastante sensible para que los resultados obtenidos bajo esta base se aparten notablemente de la verdad. La aceleración del péndulo, según las experiencias del capitán Sabine, se manifiesta regularmente en los terrenos volcánicos, y el retraso en los terrenos areniscos y arcillosos; de modo que la incertidumbre que reina necesariamente sobre las observaciones del mismo viene a afectar a todos los cálculos fundados sobre ellas.
Presentemos esta teoría en un orden científico más rigoroso. Para esto, concibamos un esferoide fluido, poco diferente de la esfera, y compuesto de un número cualquiera de capas de diversas densidades, cuyas partes todas se atraigan mutuamente en razón directa de sus masas e inversa del cuadrado de sus distancias. Ya veremos a su tiempo qué tal es el caso de la Tierra. Demos a este cuerpo un movimiento de rotación uniforme en derredor de un eje fijado sobre su superficie, e investiguemos la figura que esta superficie, así como las capas interiores, deberán tomar para conservarse en equilibrio relativo entre ellas bajo la doble influencia de las atracciones moleculares y de la fuerza centrífuga nacida del movimiento de rotación. Claro es que en este caso la forma exterior de la masa fluida y la ley de la pesadez en la superficie se hallarán ligadas entre sí por una mutua dependencia. El estado actual del análisis no permite determinar esta relación en la generalidad con que acabamos aquí de enunciar el problema. Empero Newton había logrado descubrirla en el caso de la homogeneidad; y Clairaut ha conseguido también calcularla en el caso, mucho más general, de que el esferoide esté compuesto de un número cualquiera de capas elípticas de densidades arbitrariamente variables. Entonces la intensidad de la pesadez y las longitudes de los grados de meridiano van creciendo desde ecuador hasta el polo, proporcionalmente al cuadrado del seno de la latitud; al paso que los radios tirados desde el centro decrecen, por el contrario, según la misma ley, y existe entre la variación total de la pesadez y la de los radios esta relación notable: Dividido que sea el exceso de la pesadez en el polo sobre la pesadez en el ecuador por esta última, y dividido que sea igualmente el exceso del eje del ecuador sobre el eje del polo por este último, se forman dos fracciones cuya suma es contante y siempre igual al doble del achatamiento que el esferoide habría debido tomar en el caso de la homogeneidad, conservándose la misma duración de su rotación. Si se supone ahora que esta primitiva fluidez y esta distribución regular de las capas fluidas han sido el estado originario de los cuerpos planetarios; si se supone además que entre todas las figuras de equilibrio posibles poco diversas de la esfera estas capas han tomado la elíptica y conservándola solidificándose; por último, si se admite que la pesadez en la superficie del esferoide haya también conservado precisamente la intensidad que tenía antes de la solidificación, sin que ninguna revolución interior extraña a la formación de esta superficie la haya modificado con posterioridad, es patente que entonces las relaciones indicadas por la teoría de la atracción para los esferoides elípticos se hacen completamente aplicables, y que el achatamiento de la elipse puede ser igualmente determinado y debe conducir a un valor semejante, sea por las longitudes del péndulo, sea en fin por el cálculo de la influencia que el achatamiento ejerce en los movimientos de los cuerpos lejanos sobre los cuales obra el esferoide por atracción. Pero todos estos supuestos son necesarios para que las relaciones propias a la elipse existan entre las medidas del péndulo y las de los grados, o aun en cada uno de estos fenómenos separadamente. Así, lo que hay que hacer no es suponerlas existentes, sino tratar de ver por la experiencia si se verifican realmente con todas sus particularidades.
Ya hemos hecho notar que los grados del meridiano medidos en diferentes partes de la Tierra se apartan notabilísimamente de las relaciones que les asignaría una regular y general figura elíptica. La teoría de la atracción muestra que este apartamiento debe ser menos sensible en las variaciones del péndulo que en las de los grados, porque en estas últimas los términos que apartan a la expresión del radio terrestre del estado elíptica aparecen afectados de coeficientes más considerables. Esto es sin duda lo que ha inducido a los geómetras a aplicar inmediatamente a las medidas del péndulo una fórmula de variación proporcional al cuadrado del seno de la latitud, de conformidad con la hipótesis elíptica rigorosa; y, por una natural consecuencia, los observadores han procurado siempre representar sus experiencias por una ley semejante de variación, cuyos resultados introducían en el teorema de Clairaut para sacar de aquí el achatamiento. Ahora pues, habiéndose hallado que los valores de este elemento así obtenidos eran en general diferentes de los que dan las simples desigualdades lunares y las longitudes de los grados del meridiano comparados entre sí a grandes distancias, ha aparecido resultar de aquí una contradicción formal, y difícil de explicar, entre estas consecuencias diversas, igualmente deducidas de la teoría de la atracción. Mas antes de llegar a este resultado, es evidente que habría sido preciso discutir desde luego las longitudes del péndulo observadas en sí mismas, independientemente de toda hipótesis sobre la constitución misma del esferoide y sobre las relaciones de la pesadez actual con la forma que la superficie ha podido tomar en el momento de la solidificación. Porque, si la ley general de variación proporcional al cuadrado del seno se manifiesta modificada en estas longitudes de una manera suficientemente seguida y sensible para no poder atribuir sus alteraciones a los errores de las experiencias, preciso será inferir que el achatamiento que se dedujere hipotéticamente de estos datos en la suposición de una figura elíptica regular, no tiene una verdadera y rigorosa aplicación física, y que así no hay ninguna necesidad de que tal combinación de números coincida, ya con la parte elíptica del achatamiento medida por la teoría de la Luna, ya con el achatamiento ideal que se sacase en hipótesis de la medida de los grados.
Los observadores que han hecho uso hasta ahora de sus medidas del péndulo, o reunídolas en general con las experiencias ya conocidas, las han tratado como resultados igualmente probables y susceptibles sólo de errores fortuitos. Porque las han fundido unas con otras por el método de los menores cuadrados, sometiéndolas a la ley de variación proporcional al cuadrado del seno de la latitud al objeto de obtener con las más leves discrepancias posibles las dos constantes propias a esta ley y deducir de aquí el achatamiento elíptico por la teoría de Clairaut. Mas esta forma general de fusión y aglomeramiento parece la marcha inversa de la que habría debido seguirse; toda vez que, en lugar de atenuar las variaciones de la ley del cuadrado del seno, variaciones que pudieran representar fenómenos verdaderos, era preciso por el contrario ponerlas todo lo pasible en evidencia para experimentar la ley misma y reconocer en la sucesión de los resultados las alteraciones que pudieran descubrir poderosas y extensas causas de atracción. Y que semejantes causas existen efectivamente y modifican en términos considerables las relaciones que deberían tener lugar en el estado elíptico, no es permitido dudarlo, discutidas que sean detenidamente y de una manera racional las principales observaciones del péndulo hechas hasta el día.
El tiempo y el espacio nos faltan aquí para entrar en esta discusión tomando por base las principales medidas del péndulo verificadas hasta el día en los principales puntos del globo. Ella nos manifiesta del modo más patente las anomalías que estas medidas presentan en los diferentes paralelos. Comparando la longitud media del péndulo observada en el ecuador con las obtenidas respectivamente para el polo y el paralelo de 45º por medio de las oportunas experiencias, se halla que ofrecen la siguiente progresión, la cual puede considerarse como el resultado más inmediato de las observaciones:
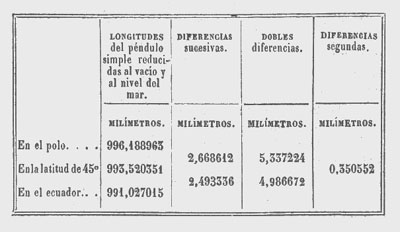
Vese aquí que las diferencias sucesivas son notablemente desiguales; mucho más de lo que lo son las observaciones individuales entre sí, cualquiera que sea la parte en que se las escoja, Este fenómeno no puede, pues, revocarse en duda; ni atribuirse a accidente alguno de localidad. Ahora bien, esto es enteramente contrario a la hipótesis elíptica. Porque siendo en ésta la variación de longitud del péndulo proporcional al cuadrado del seno de la latitud, si se representa su expresión general por
l = a + b sen2 L,
siendo a y b dos constantes, la primera de las cuales representa al péndulo ecuatorial mismo, se tendrá evidentemente
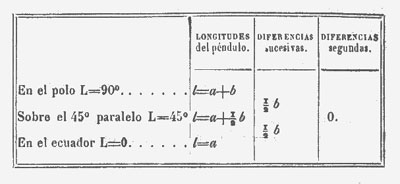
Donde se advierte que en semejante hipótesis las diferencias primeras de las tres longitudes escogidas de este modo deben ser constantes e iguales a la mitad del coeficiente del cuadrado del seno; al paso que sacando estas diferencias del conjunto mismo de las observaciones, las hallamos sensiblemente desiguales, y mayores desde el 45º grado al polo que desde el mismo punto al ecuador.
Síguese de aquí que un observador que quiera calcular el achatamiento de la Tierra por las medidas del péndulo en la hipótesis elíptica con el auxilio del teorema de Clairaut debe encontrar resultados muy diferentes entre sí, según la parte del hemisferio en que dominen las observaciones de que hace uso. Porque, por ejemplo, si combina el péndulo ecuatorial dado inmediatamente por las experiencias con el valor de la constante dada por observaciones intermedias entre el grado 45º y el polo, o entre el grado 45º y el ecuador, o por último en toda la extensión del hemisferio boreal, obtendrá los tres valores reunidos en el estado siguiente en que la letra a representa al péndulo ecuatorial 991,027015, según hemos hallado más arriba.

Lo cual confirma completamente cuanto hemos dicho acerca de la inseguridad de servirse de las medidas del péndulo para la determinación de la figura de la Tierra; a lo menos en tanto que la ley que liga las variaciones de su longitud en las diferentes latitudes, no sea más exactamente conocida.