Para conocer el procedimiento que se emplea a fin de efectuar esta iluminación y graduarla al arbitrio del observador según la intensidad del resplandor que tenga a la sazón el astro observado, pueden consultarse los tratados de Astronomía práctica. Aquí nos contentaremos con dar una idea del método usado generalmente.

Consiste en fijar delante del anteojo del instrumento o en su interior, un diafragma anular formado de un metal blanco y mato cuya parte llena cubre, sólo la del campo más próximo a los bordes y menos necesaria para la observación, y luego se ilumina lateralmente este diafragma por la luz de una lámpara que se despide por irradiación a lo interior del tubo sin formar imagen focal. Produce entonces en el fondo del ojo una impresión general y simultánea con la del punto radiante que se observa, e interrumpida sólo en la proyección de cada hilo, de modo que el lugar de estos viene a ser perceptible por ocultación cual si fuera de día. Como esta luz añadida debilita la sensación que habría producido el punto radiante sobre el fondo negro del campo del anteojo, se buscan los medios de graduar su fuerza para que el mismo no desaparezca. Si el diafragma está delante del anteojo, como en la mayor parte de los instrumentos portátiles, se consigue fiando la luz a un ayudante que la aleja o aproxima según la necesidad. Empero si es interior, según sucede generalmente en todos los instrumentos fijos, se hace llegar el resplandor de la lámpara por una abertura practicada en el eje de rotación horizontal del anteojo, y más acá se establece como aparato moderador un diafragma de abertura variable compuesto de dos chapas metálicas que pueden cubrirse mutuamente y disminuir aquella por la cual llega la luz hasta interceptarla del todo, si se quiere. Esta especie de pupila artificial se mueve por una tira cuyo extremo cae cerca del ocular y a la mano del observador. (N. del T.)

Circunscribímosnos aquí a indicar este método, porque es muy sencillo, muy exacto también, cuando la marcha del reloj es bien conocida por observaciones de pasos hechos anteriormente en el vertical próximo al meridiano en que primeramente se había fijado el eje óptico, y por último, porque no requiere noción alguna astronómica anticipada. Pero luego que se han establecido las leyes del movimiento diurno y se puede lógicamente hacer aplicación de ellas, la observación de los pisos sucesivos de diferentes estrellas, desigualmente distantes del polo visible, ofrece procedimientos más porque las diferentes épocas de estos pasos varían el azimut del vertical en que se los observa; y de aquí puede inducirse con mucha exactitud el valor angular de estos azimús por observaciones que, durando sólo algunos instantes, pueden repetirse tantas veces como se crea necesario. Cuando el vertical del paso ha sido traído así sumamente cerca del meridiano, y su desvío azimutal ha llegado a ser tan pequeño, que con dificultad puede esperarse corregirle por movimientos mecánicos, se determina su valor por el sistema de observaciones que acabamos de indicar, y se le toma en cuenta por el cálculo en los ulteriores resultados dados por el instrumento. Si este desvío llega a experimentar luego algún cambio por efecto de todas las causas físicas a que está siempre sometido un instrumento material, se apercibe uno al punto de ello por este mismo género de observaciones, o trayendo el anteojo sobre la mira fija; y si el dicho desvío se ha hecho demasiado manifiesto, se le corrige, o se contenta uno con estimarle por el cálculo, si es del orden de errores que llevan consigo los movimientos mecánicos. Porque nunca repetiremos demasiado que no puede alcanzarse jamás el último grado de precisión sino por correcciones abstractas, nunca por un procedimiento manual. Por igual motivo, cuando se trae al eje de rotación sumamente cerca de la horizontalidad y se mantiene estable en tal estado, es preciso guardarse mucho de retocarle a cada paso, siendo infinitamente más seguro tener en cuenta su inclinación por el cálculo que probar a hacerla nula físicamente. (N. del A.)

Sobre este punto pueden consultarse las obras de Astronomía práctica. (N. del T.)

Llamando An al azimut del astro contado desde norte hacia el este, Z a la distancia zenital, D a la distancia del polo al zenit en el lugar de la observación, y @ a la distancia polar, tendremos por las formulas de la trigonometría esférica:

cos @=sen Z sen D cos An + cos Z cos D

cuya expresión para simplificar el cálculo se trasforma en estotra:

sen2 I/2 A=sen2 I/2(Z-D) + sen Z sen D sen2 I/2 A

(N. del T.)

Estas observaciones han sido calculadas tomando la distancia D del polo al zenit igual a 51º53´14´´,5 como Piazzi la había deducido de las distancias zenitales de las estrellas circumpolares observadas así encima como debajo del polo, y corregidas de las refracciones del momento que las afectaban en cada paso. La primera de las distancias @, mencionada como propia de cada estrella citada en el estado anterior, había sido igualmente determinada por las distancias zenitales de la misma observadas en su paso meridiano y corregidas de la refracción que actualmente las afectaba. (N. del A.)

Las fórmulas que sirven para hacer este cálculo, son:

sen I/2 A= 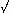símbolo sen(@+D-Z/2)sen(@+Z-D/2)

sen Z sen D

sen I/2 S= 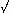símbolo sen(D+@-Z/2)sen(D+Z-@/2)

sen Z sen @

sen I/2 P= 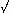símbolo sen(Z+@-D/2)sen(Z+D-@/2)

sen @ sen D

en que D es la distancia del polo, Z la del astro, @ su distancia polar, S el ángulo en el astro, y P el ángulo en el polo. (N. del T.)

Esta fórmula no puede aplicarse inmediatamente más que a los astros que no tienen movimientos propios; respecto de los otros es necesario tener antes en cuenta el efecto de este movimiento sobre el ángulo P durante el tiempo t. Daremos ejemplos numéricos en su aplicación en estos dos casos, cuando hayamos descrito minuciosamente el modo de observar con los círculos repetidores portátiles, uno de cuyos principales usos es cabalmente dar el tiempo absoluto, o el ángulo horario P por la medida de las distancias zenitales tomadas fuera del meridiano. (N. del A.)

Indicaremos brevemente el procedimiento que se sigue, para esta determinación.

La expresión analítica de la refracción, expresada en segundos de grado para alturas aparentes de más de 120 sexagesimales, es la siguiente:

a p tang Z/0,76. (1+t. 0,00375) - a p/0,76.0,00125254 tang Z/cos2 Z + I/2 a2 sen 1.´´ p2/[0,76(1+t. 0,00375)]2 (1+2 cos2 Z) tang Z/cos2 Z

en la cual Z es la distancia zenital observada bajo la presión barométrica p y a la temperatura t, expresada la primera en partes de metro y la segunda en grados del termómetro centesimal. Todo es pues conocido en esta fórmula, a excepción de a que representa un coeficiente constante, y se determina por las observaciones de estrellas circumpolares.

Sean para esto Z la distancia de una de estas estrellas al zenit en su paso por el meridiano superior, y Z´ esta misma distancia para el meridiano inferior observada desde el propio punto de la tierra. Las refracciones r y r´, correspondientes a ambas, podrían calcularse por la indicada fórmula si se conociese a a. Pero no conociéndola, se puede calcular siempre los demás coeficientes numéricos que la multiplican en la fórmula y dependen sólo de la distancia al zenit, de la presión y de la temperatura, datos ofrecidos por la observación. Así, y dentro de los límites de las distancias zenitales a los cuales es aplicable aquella, se tendrán para r y r´ expresiones de esta forma:

r=Aa+Ba2 r´=A´a+B´a2

en que A, B, A´ y B´ designan números conocidos. Las distancias zenitales verdaderas corregidas de las refracciones estarán pues expresadas por

Z+Aa+Ba2, Z´+A´a+B´a2

Y si estas distancias están bien corregidas, su semisuma debe dar la verdadera distancia del polo al zenit, la cual llamaremos D. Se tendrá pues sumándolas:

Z+Z´+(A+A´)a+(B+B´)a2=2D

En esta ecuación sólo a y D son desconocidas; cada estrella observada por encima y por debajo del polo dará otra semejante; y como a y D son las mismas para todas las estrellas, dos de dichas ecuaciones bastarán para determinarlas, es decir, para conocer la distancia verdadera del polo al zenit y el coeficiente a de la refracción. No conteniendo ya entonces la fórmula ningún dato indeterminado, se podrá calcular su valor para todas las distancias zenitales, de grado en grado, y formar tablas de refracción dentro de los límites establecidos.

Como aquí se supone que la distancia polar de cada estrella es la misma en ambos pasos por el meridiano, siendo así que estas distancias varían por efecto de la precesión, de la aberración y la nutación, es menester corregirlas de estos efectos para hacerlas comparables entre sí, o a lo menos las variaciones que de ellos han debido resultar en las distancias zenitales durante el intervalo de tiempo en que se han hecho las observaciones. Esto es lo que se llama reducir las observaciones a la misma época. (N. del T.)

Sean R el radio del ecuador de la esfera celeste y r del paralelo. La cuerda que subtende el ángulo E sobre el círculo ecuatorial es 2R sen 1/2 E; aquella que subtende el ángulo P sobre el contorno del paralelo es 2r sen 1/2P. Toda vez que éstas cuerdan deben ser iguales en su superposición, la expresión de esta igualdad será:

R sen 1/2 E = r sen 1/2.

Sea d la distancia polar del paralelo, se tendrá

r = R sen 1/2 d;

sustituyendo este valor, y dividiéndolo todo por R resulta

sen 1/2 E = sen d sen 1/2 II (1);

que es la fórmula exacta general y rigorosa. Empero cuando los ángulos E y II son muy pequeños, la relación sen 1/2 E/sen 1/2 II es casi la misma que la de E/II. Así que sustituyendo esta relación a la primera en la ecuación anterior, se reduce a

E = II. sen d (2)

que es la que hemos empleado; mas sólo es aplicable a ángulos muy pequeños.

Admitiéndola como suficientemente exacta, llamemos T al intervalo de tiempo sideral que deba invertir una estrella en recorrer el ángulo E del círculo ecuatorial, y t aquel que otra situada sobre el paralelo tarde en describir el ángulo II. Debiendo ser recorridas en 24 horas siderales las circunferencias de ambos círculos, se tendrá por proporción

T = 24k E/360º t = 24k II/350º;

luego

T = t E/II = t sen d.

Es la relación que expresa el estado inserto arriba, y la cual resulta así comprobada experimentalmente.

Conviene notar que el radio R de la esfera celeste ha desaparecido de la ecuación (1), en términos que las reducciones de los arcos E, II y d, son independientes del valor del mismo. Era fácil de preveer, puesto que todas las esferas concéntricas que pueden describirse así en torno del observador, no alteran los valores absolutos de los ángulos, y sí sólo las de sus senos. Mas como éstos crecen todos al propio tiempo en la misma relación, y proporcionalmente al radio de la esfera alteran por esto las relaciones de magnitud subsistentes entre ellos, y se refieren solamente a una unidad diversa. Así que, desaparecerá siempre el valor absoluto del radio de la esfera en las ecuaciones que tales relaciones expresan. Aunque esta observación es muy sencilla, nos ha parecido útil presentarla para hacer comprender mejor con este ejemplo que lo que se llama esfera celeste no es más que un concepto geométrico, propio para fijar los razonamientos, y que no se debe unir a él ninguna idea de realidad física o magnitud absoluta. (N. del A.)

Sean P la diferencia de las ascensiones rectas de los dos astros, o el ángulo en el polo comprendido entre sus círculos de declinación; @´, @´´ sus distancias polares respectivas, y D el arco de círculo máximo que mide su distancia angular sobre la esfera celeste. Si se considera el triángulo esférico formado por los tres lados @´, @´´ y D, en él se conocerán @´, @´´ y el ángulo comprendido P. Aplicadas a este caso las reglas de la trigonometría esférica, darán

cos D = sen @´ sen @´´ cos P + cos @´ cos @´´.

Si se sustituye a cos D, cos P, y luego a los (@´´-@´) con sus equivalentes

1-2 sen 2 1/2 D, 1-2 sen 2 1/2 P, 1-2 sen 2 1/2 (@´´-@´),

se transformará dicha expresión, y se obtendrá estotra mas cómoda para el cálculo numérico

sen 2 1/2 D = sen 2 1/2 (@´´-@´) + sen @´ sen @´´ sen P.

Más adelante tendremos ocasión de reconocer que el polo cambia de posición entre las estrellas en el trascurso de los siglos, lo que hace variar desigualmente sus distancias polares y ascensiones rectas absolutas; pero comprobaremos también que este movimiento pertenece en realidad al eje de rotación de la Tierra, y que las estrellas no participan de él. Sus distancias relativas D, calculadas por la fórmula anterior, no pueden pues cambiar sino por efecto de los movimientos individuales que fuesen propios en las aquéllas. El cálculo de la distancia D, reiterado para épocas muy diversas entre sí, con los valores de @´ @´´ y P en ellas observadas, presenta, pues, un medio directo de comprobar la existencia y medida de estas variaciones. Por desgracia las observaciones antiguas hechas antes de la invención de los instrumentos de anteojo y relojes de péndulo son harto inexactas para hacer de ellas aplicaciones tan minuciosas; sólo puede inferirse de ellas que los movimientos propios de las estrellas deben ser muy pequeños, toda vez que las configuraciones de los grupos en que se los reúne bajo el nombre de constelaciones presentan, aun hoy, las mismas apariencias que les han dado los astrónomos griegos. Considerándolos entonces como despreciables en comparación de los errores que debían envolver las antiguas observaciones, puede estimarse la extensión de estos errores calculando los valores que dan las mismas para las distancias D, calculadas por nuestra fórmula, y comparándolos con aquellos que determinamos hoy con mucha más exactitud, a fin de ver en cuánto discrepan. (N. del A.)