—[42]→ —43→
Dept. of Hispanic and Italian Studies
The University of British Columbia
1866 Main Mall
Vancouver, B.C. V6T 1Z1
Canada
In the last two or three decades, chaos scientists
have been coining new words and adapting
words from every-day language to name and
describe some characteristics of mathematical
entities and physical phenomena, as revealed
in images generated by computers4. «Science
takes words and shapes their meaning to its
own ends»
, states Ian Percival (16) and, apparently,
humanities can play the same game by reclaiming the
words shaped by science and reshaping them to serve their own
purposes. «Fractals», «attractor», «cascading», and other terms as
—44→
common as «sink», «doughnut», «saddle», and «noise», which have
clear and specific meanings for chaoists, have been adopted by
literary critics and are now being used in their scientific context to
describe aspects identifiable with written discourse. The methodologies
and instruments of enquiry used by scientists and literary
critics are, on the other hand, entirely different.
Chaoists rely heavily on powerful machines to carry out in minutes the wearying and time-consuming iterations required to plot and make dynamically visible on the screen the trajectories produced by instructions programmed into the computer. This reliance on, and extensive and unavoidable use of, computers make the transition from science to humanities difficult. How to feed into a number-crunching machine intangibles which cannot be represented by numbers or formulas, purporting to obtain results akin to those obtained by scientists handling hard data? How to convince scientists of the validity of the subjective conclusions reached by humanists handling the soft data drawn from the imaginary worlds which are their concern?
Humanists and scientists deal with their interests in totally
different ways, and their analogies reflect these differences in
approach. For instance, mathematician Ian Stewart has no qualms
whatsoever at mixing Italian cooking and cosmology in order to
bring his point home. The stars that move within a galaxy whose
trajectories fall apart are, in the words of Stewart, «meatballs of regularity
in a stochastic spaghetti»
(151). The reason why Stewart's
comparison is successful is because it allows both scientists and
non-scientists to visualize the physical problem instantly. Virtually
everyone reading Stewart has seen a dish of spaghetti and meatballs,
or has a close idea of what it looks like, or can imagine how
a dish of spaghetti and meatballs probably looks from the description
of the problem involved in tracing the trajectories of stars
within a galaxy as described by Stewart. Scientists, it would seem,
can contain the universe in a pasta dish in the laboratory and get
away with it because they can imagine and devise mathematical
formulas to describe their theories, and most scientists are able to
carry out and repeat experiments in their laboratories, or against
real phenomena, to validate or disprove their hypotheses. There
is, however, one small kink etched on the scientific side of the coin.
—45→
When the time came for Stewart to represent «the restricted three-body
problem, in an approximation due to Hénon and Heiles»
(150, Figure 59), he could not resort to a drawing, however schematic,
of a dish of spaghetti and meatballs. His comparison would
have collapsed. Scientists can visualize galaxies and describe them
as dishes of spaghetti and meatballs, but they are hesitant to draw
them as a culinary concoction, and they certainly cannot test a
literary work in a scientific laboratory.
As a rule, the material and data handled by artists, critics, and philosophers can seldom be tested in laboratories; theories can neither be conclusively proven nor altogether dispelled. The way non-scientists bring their points home most forcefully is, not infrequently, by simply reversing the order of the two terms of the scientist's equation. A poet would compare the eyes of his beloved to the stars in the sky; a gastronomer a dish of spaghetti and meatballs to heavens. Artists can visualize, paint, dissect, draw, and sculpt ethics, virtue, truth, and God and write next to them the words ETHICS, VIRTUE, TRUTH, and GOD as a matter of fact. No wonder, then, that artists, philosophers, and literary critics have visualized Don Quixote by cutting it up in sections and have, taking advantage of the loophole that humanities have over sciences, painted, played, sang, and made terra-cotta and marble models of countless, isolated components of Cervantes' work, writing next to them: DON QUIXOTE, DULCINEA, THE ENCHANTED INN, SANCHO, ROCINANTE. They, however, have not as yet imagined or conceptualized this work of Cervantes' as a whole and, consequently, have not as yet been able to envision a metaphor similar to Stewart's dish of spaghetti and meatballs comparing Don Quixote to, let us say, a dish of paella, nor have they conceived the thought of writing the words DON QUIXOTE next to the drawing of an attractor5.
You «cannot use the theory of chaos everywhere»
, warns
Percival. «The state of Eastern European politics may look chaotic,
but you cannot study a subject of this type using chaos theory.
—46→
There are many other situations that are chaotic in the ordinary
sense, but not in the scientific sense of chaos»
(16). Only figuratively,
therefore, may a work of fiction be compared, for instance,
to a generic land windstorm, in the sense that a work of fiction has,
like any tornado, its own characteristic features, is dependent on
a great number of variables (authorial, compositorial, editorial, critical),
and frequently appears pulling and dragging some critical
apparatus behind it. The similarities between these two phenomena
increase when one realizes that, just as the foreign debris
picked up by a tornado in its path inserts in the system variables
previously unaccounted for, variables which produce minor,
localized disruptions without altering the overall behavior of the
phenomenon permanently, so does the critical apparatus appended
to literary works.
As just one of the tens of millions of such entities, Don Quixote, the specific subject of this study, may be regarded as a dissipative system, and literary critics may be tempted to approach Cervantes' discourse as meteorologists approach natural phenomena. The caveat, however, is crystal clear: Don Quixote is not a natural phenomenon. Hence, the meanings of the words «system», «chaos», or «stochastic», as used by a scientist are not even remotely comparable to the meanings of the words «system», «chaos», or «stochastic» when these terms are applied to Don Quixote or its characteristic features. Imagination may accept the two identical terms of each set as comparable, Nature does not. And yet, the temptation to equate two completely different things metaphorically, a passage from Don Quixote, for example, to the turbulence of a waterfall (forced dissipative hydrodynamic flow), or the smooth flowing of another passage to the seemingly gentle current of a river, is overwhelming; even though the turbulence and the gentle flow one may discern in writing cannot, in fact, be either turbulent or gentle from a scientific point of view. There is, however, a direct connection between the two terms of such a metaphor; the disturbing turmoils and calm courses of written discourse are the «system of equations» that represent the biochemical processes that were taking place in the mind of the author at a certain period in real time during the conception, penning, and revisions of his work. Don Quixote (1605, Part I; 1615, —47→ Part II) is, in other words, the written equation of the portrait's time of Cervantes' thought, just as Van Gogh's Eight Self-portraits (1886–90), Rodin's Le Penseur (1904), and Gehry's Guggenheim Museum, Bilbao (1998) are the topographical equations of the portraits' time of these artists' thought. True, we cannot even dream of ever attaining an exact portrait of any of the processes of creation from which Don Quixote, «Eight Self-portraits», Le Penseur, and the Guggenheim Museum arose; but neither can we dream of ever obtaining the complete portrait of the ongoing processes of transformation taking place in the Milky Way. Chaos theory can, therefore, be also applied in the humanities. Its elegance, simplicity, and sheer beauty makes chaos theory, in my opinion, the ideal vessel from which to envision the creative processes innate in each work of art and the ideal medium to represent these processes and their outcome graphically.
Each work of art is, of course, a distinct individual. A literary work, for instance, is made unique by the characteristics innate to written discourse, its author, and its particular milieu: language, orthography, style, syntax, genre, narrative skills and strategies, humor, plot, social context, etc. These literary aspects cannot be dispensed with in the great majority of critical studies dealing with a written work of art but, since the concept of chaos must be approached as a unifying theory, these purely literary aspects should be seen simply as the outside parameters of a study based on chaos theory. That is to say, the aim of a study such as this should be to keep to a respectful distance not only those elements that make one specific work of art different from another but, also, all those elements which make art, sciences, humanities, theology, and technology seem alien from one another. Its initial aim should be to simplify, so that by eliminating all differences between disciplines a common denominator may be found with which all products of human endeavor may identify. Chaos theory should be applied to the paintings of Stella, Pollock, and Gorky, let us say, to Norman, Gothic, and Gaudí's architecture, and to the tonalities of Asian, European, and African rhythms, not to explain them or to find order in their «chaos» but, rather, to reach an essence they have in common and represent it graphically in portraits totally unlike the paintings, buildings, and musical scores that inspired —48→ them, just as a trajectory being plotted on the screen of a computer is entirely unlike the mathematical formula that is generating it6. My goals here are: (1) to conceptualize Cervantes' novel as a whole, (2) to envision the creative process, and (3) to write DON QUIXOTE next to a drawing of its attractor.
Within a deterministic frame of reference, I consider «formulart»
to be both the essence of all works of art and the space within
which all works of art fall7. In this pristine state, the entire work of
art already exists as an idea in the mind of its author. This hypothetical
state is a dot representing the precise moment preceding
the slow and laborious transformation of an idea into a physical
entity, be it a still life, a novel, a bust, a symphony, or a cathedral.
In the case of a written, literary work, «formulart» is a universe of
thoughts compressed into an infinitesimally small dot a microsecond
before the ideas begin to transform and expand into
written symbols, creating their own finite time and space until the
unformulated text results in the literary work it was meant to be
from the very beginning. In order to prefigure the imminence of
the process about to take place, «formulart» may be drawn as a
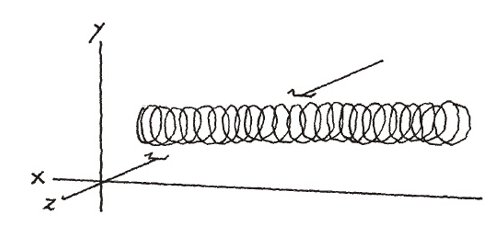
flexible, free floating entity. And given that a coil may assume an
endless variety of shapes without suffering any distortion  , a free-floating coil seems to be an ideal entity to
represent a work of art in its pristine state. It seems to me,
therefore, that a horizontal, straight, free-floating coil, as portrayed
in Figure 1, is the more apposite shape to represent the idea which
would later on become Don Quixote.
, a free-floating coil seems to be an ideal entity to
represent a work of art in its pristine state. It seems to me,
therefore, that a horizontal, straight, free-floating coil, as portrayed
in Figure 1, is the more apposite shape to represent the idea which
would later on become Don Quixote.
Figure 1. A three-dimensional, phase-space portrait of literary «formulart».
The printed text itself may then be represented as a finite cylinder encasing the literary work, Figure 2.
Figure 2. The manuscript or printed text as a finite cylinder encasing literary «formulart».
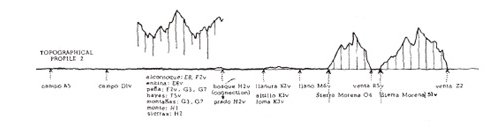
My primary concern when dealing with Cervantes' writings has been to explain away aspects of apparently chaotic behavior in both «formulart» (irregularities of a narrative character) and the encasing cylinder (orthographic randomness). For instance, to make visually accessible to my readers some of the textual inconsistencies one finds in Part I of Don Quixote, I draw a topographical profile of this section of the work showing «ghost mountains» floating over what originally had been the rolling hills of La Mancha («Cervantes at Work», Plate between 144–45), Figure 3. But only until recently did I realize that the underlining purpose of my studies has always been to make evident the fact that —50→ in Cervantes chaos is, simply, another realm of order.
Figure 3. Topographical profile of chapters 1-37 of Don Quixote, Part I.
Another example: by following the setting and printing processes that culminated in the first editions of Part I and II of Don Quixote in some detail, I was able to explain, amongst other puzzling textual and stylistic characteristics of Cervantes' works, the reasons that lie behind the chaotic behavior of textual components. The orthographic chaos (spelling and punctuation vagaries) evident in Don Quixote, Parts I and II, resolved, to paraphrase Stewart's description of stars moving within a galaxy (150), in a string of forty-seven islands of relative regularity sitting in a complicated way in a stream of chaos. I illustrated my findings by drawing a phase-space representation of the distribution of labor between the compositors, Figure 48.
Figure 4. A representation of the division of labor between compositors C, D, E, F, H, I, and J of the first editions of Don Quixote, Parts I and II.
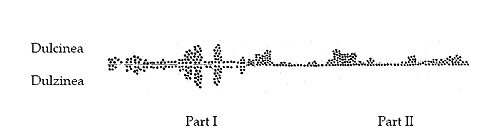
This phenomenon may be illustrated more vividly by following the ups and downs suffered by a word travelling through the stream —51→ of chaos. The two forms of the word «Dulcinea» (Dulcinea/Dulzinea) may be followed, for instance, as they move through four cylinders representing the first (A), second (B), and third (C) Madrid editions of Don Quixote, Part I, and the first edition of Part II (D), Figure 59.
Figure 5. Occurrences of the spellings Dulcinea/Dulzinea in the first (A), second (B), an third (C) Madrid editions of Don Quijote, Part I, and the first edition of Part II (D). For each, the dots above the line represent appearances of Dulcinea, and the dots below the line of Dulzinea.
Figure 5 portrays the process of «regularization» that the form «Dulzinea» underwent in the early Madrid editions of Don Quixote10. —52→ Because we can be certain that it was not Cervantes who changed from one spelling (Dulzinea) to the other (Dulcinea), we can safely conclude that the apparently chaotic spelling behavior reflected in Figure 5 is the result, initially (A), of compositorial ambivalence as to the most «appropriate» spelling, subsequently (B and C), of compositorial orthography being imposed over the original spelling and, lastly (D), of the authorial spelling having been replaced entirely with the form preferred by the compositors11.
When portraying the overall orthographic disarray found in the text, the only aspects that must be taken into consideration are: (1) the spellings that exhibit deterministic-chaotic behavior, (2) the corresponding numbers of occurrences, and (3) the gatherings where the occurrences appear; therefore, if one eliminates from Figure 5 the gatherings where no occurrences of the word Dulzinea/ Dulcinea appear, superimposes the resulting graphs of stages A, B, and C, and joins them with the resulting graph of stage D, the representation of all stages compounded is a fair portrait of the overall orthographic disarray one finds in the text of the first three Madrid editions of Part I and the first edition of Part II, Figure 6.
—53→Figure 6. A representation of the text of Don Quixote showing the process of «regularization» in the spelling of the two-form word Dulcinea (upper portion) and Dulzinea (lower portion).
Figure 6 clearly shows that the area of conflict between the authorial and the compositorial spellings of the two-form word Dulcinea/Dulzinea in Don Quixote is located in Part I exclusively. Since each word having more than one spelling form behaves differently from every other similar word, the representations of the text shown in Figures 5 and 6 are valid only in respect to the single term already considered. However, when one tabulates and draws the behavior of the spellings of other words with more than one spelling form, the resulting graphs show also more activity in Part I than in Part II. And if we project these tabulations on the entire length of Don Quixote, the resulting drawing shows that the sections of the system where the behavior of differing spellings seems more chaotic are the areas located at the beginning and in the middle of Part I, Figure 7.
Figure 7. A representation of the text of the first editions of Part I and II of Don Quixote showing the area where the chaotic behavior of differing spellings is more pronounced.
The «lopsided random smudge of dots» represented in Figure 7 brings to one's mind the image of a spiral galaxy seen from one —54→ side of the system12. Unlike natural galactic systems, however, the galaxy portrayed in Figure 7 is neither an expanding stellar system nor a galaxy in the process of being swallowed into a black hole, but, rather, a closed, or contained, structurally-stable word system which can no longer contract or expand. This particular system would experience, none the less, periodic, internal disturbances caused by regularization and/or modernization, because Don Quixote, like all literary works, has always been, and will for ever be, at the mercy of its copyists, compositors, publishers, and editors.
The portrait of Don Quixote projected in Figure 7 posits one fundamental question: what is it that stands at the gravitational center of Cervantes' novel holding the entire system together and keeping it structurally stable? To answer this all-encompassing query one must: (1) define the outside parameters of the equation, (2) draw out a clear signal by eliminating all interfering noise, (3) find the constant(s) and variable(s) that control the process, (4) tabulate these features, and (5) draw a portrait of the phenomenon.
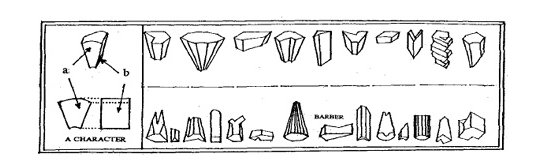
Let us deal, first, with some of the obtrusive noise. Were one to be asked to name the most important component of Cervantes' fable, one would in all probability be urged to answer «Don Quixote» immediately, with a clear, resounding, and definitive tone to it. The reason behind this confidence is that Don Quixote, Alonso Quijana, the Good13, the Peerless Knight of La Mancha, the Knight of the Mournful Countenance, the Knight of the Lions, the Protector of Beguiled Damsels, the Savior of Infantes in Distress, the epitome of the Romantic Hero and Lover, in short, a product of Cervantes' imagination, has clearly transcended «formulart», encasing cylinder, and even the name of its creator in the minds of —55→ painters, writers, sculptors, composers, literary critics, and philosophers. This commonly-held misconception is understandable, but it stands on very fluxional grounds. There is no question whatsoever that Don Quixote is the most visible character in the fable, but it must be kept in mind, too, that Cervantes left his Knight out of the story in several occasions and that the role of Don Quixote in many other episodes is, at best, marginal. Several other fascinating characters are, moreover, intermittently vying for our attention, Figure 8.
Figure 8. Portraits of some characters in Don Quixote14.
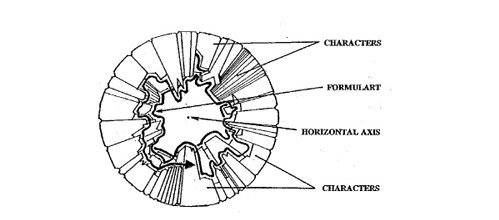
The different «shapes» illustrated in Figure 8 are the signatures —56→ that represent the uniqueness and relative importance of each character. By tessellating the curved, outer facets of the characters' on the outward surface of the cylinder encasing «formulart», so that their «bodies» point towards the horizontal axis of the cylinder, we obtain more detailed images of both the casing and «formulart», Figures 9, 10, and 11.
Figure 9. Two views of a section of the casing cylinder with some of the characters.
Figure 10. An end view of the casing cylinder showing some of the characters, «formulart», and the horizontal axis in Don Quixote.
—57→Figure 11. Three different views of a section of the casing cylinder showing «formulart» and the horizontal axis. Arrows indicate the direction of flow (progression of the work)15.
The characters are within the casing cylinder, all with their outer faces at the same level, and, as a unit, they serve two very important functions in Don Quixote: (1) they decorate the smooth, resilient outer face of the container with their outward looks and (2) they define, limit, and reshape with their «bodies» and location the hypothetical, idealized, ordered behavior of «formulart» as illustrated in Figure 1. With the shapes and depths of their personalities, the characters make visually evident the turbulent and unpredictable nature of the creative process as reflected in the text (Figures 10 and 11). But the characters are too numerous and appear too randomly distributed for any one of them to be the variable, or stand out as the constant, that controls Don Quixote. To find these determining aspects of the system one must return to the patterns plotted by the processes of authorial creation and revision.
The numerous and substantial authorial alterations made to the text of Don Quixote -including the division into chapters, the interpolation of extraneous material, and the deletion of key passages- were introduced during the writing of the early chapters of Part I and show more clearly in this section of the work —58→ (Figure 3). This eccentricity strongly suggests the possibility that some sort of irregular process is taking place in Don Quixote. And, more to the point, the very existence of these irregularities points to a possible dependence of the system on initial conditions. The query is, then: what conditions?
The stories narrated in Cervantes' novel take place in turn-of-sixteenth-century Spain, Algiers, and Italy, i. e., in areas with well-defined geographical, historical, and chronological parameters. The configuration and location of the casing's horizontal axis (a straight line equidistant to all points of the cylinder; Figures 10 and 11) reflects the synchronization of the spatial, contextual, and temporal elements within the system. We have, on the other hand, a fictional, Manchegan hidalgo who decides to use this perfectly balanced springboard as a trampoline on which to carry on a chivalric quest characteristic of earlier centuries, Figure 12.
Figure 12. Starting configuration for Don Quixote (a) and resulting trajectory (b). The 0's represent historical, sixteenth-century Spain, the 1 represents the imaginary world of chivalry in which Don Quixote moves16.
The anomalous trajectory taken by the story is, therefore, the result of an «error» planted in the system's program to produce the parting, meeting, and intermittent reconciliation of two initially harmoniously-adjacent behaviors (a fictional hidalgo in sync with —59→ his milieu and a «real» Knight engaged in «real» battles of chivalry in historical sixteenth-century Spain). Thus, the perturbation introduced in the literary formula of the system is not an ineffable contrast between fiction and reality but, rather, a pulsating anachronism plausible in real life. This possibility is evident in the fact that the system recovers its original equilibrium, not as the aftermath of Alonso Quijana's dying (II, 74, 39719) but, pointedly, as the result of Don Quixote's renouncing his chivalric persona (II, 74, 39565). It is there and then that the two initially harmoniouslyadjacent behaviors finally join and run together anew, never to part again. It follows, therefore, that the attractor representing Don Quixote is in all probability an entity defined by, and existing within the boundaries of, the constant (Alonso Quijana and his historical milieu) and the variables (the victories and defeats of the Knight's out-of-sync quest).
But, what exactly is a triumph and what a defeat in the context of Cervantes' work? Are the moral (Don Quixote seeks Maritornes with sex on his mind and is rejected by her), psychological (Don Quixote suffers the ignominy of having to wear stockings with runs on them), and ethical (a Knight fighting peasants) niceties attached to chivalric demeanor and courtly love to be taken into consideration when deciding whether or not an event should be included? Should Don Quixote's success in finding the appropriate names for his horse and lady be considered triumphs? Should the burning of Don Quixote's library be considered a defeat? The answer to these conundrums is quite simple. In addition to having Don Quixote as a participant, weapons (including parts of the body) must be used or brandished and/or some sort of physical or psychological pressure must be exerted directly on Don Quixote for the event to qualify as a triumph or a defeat; therefore, none of the five passages mentioned above qualifies as an event to be considered in this context. All the events that fulfil the simple conditions stipulated above appear listed in chronological order in Table 1. The magnitude assigned to each episode varies from 0 to 10, and takes into consideration five features of the event: (1) property and personal damage incurred, (2) number and personal idiosyncrasies of the participants, (3) whether the episode is imaginary (dream, fantasy), real, or a mixture of both, (4) weapons —60→ used, and (5) further non-violent repercussions in the story. Each episode was evaluated on its own merits, but other related triumphs and defeats were also considered. For instance: the episode of the «helmet of Mambrino» (item 18) was given a 2.0 magnitude, whereas Don Quixote's attacking some flagellants was given a 7.1 magnitude. This discrepancy may seem questionable. However, since the free-for-all melee in the inn (item 25; 6.8 magnitude) is a continuation of the earlier attack on the barber (item 18; 2.0 magnitude), both magnitudes should be consider together. In other words, the episodes of the «helmet of Mambrino» have, together, a 8.8 magnitude in total, whereas the episode of the flagellants, which has no continuation, was given a lower over-all magnitude. Since no event in Don Quixote is identical to any other event, either in length or character, no repetition of the same amplitude or magnitude can occur, regardless of what values one may assign to the different events. (Refer to footnote 9).
| Event (Chapter and page) | Magnitude | |
| Don Quixote, Part I | ||
| 1 | destroys his improvised helmet with one slash of his sword (1; 25) | 0.4 |
| 2 | hits two muleteers on their heads with his lance; their friends throw stones at him (3; 38–39) | 6.2 |
| 3 | rescues Andrés from the lashing Juan Haldudo was giving him (4; 43–45) | 5 |
| 4 | is beaten by a muleteer travelling with some Toledan merchants (4; 48–49) | 7 |
| 5 | fights and is winning in an imaginary tournament; the priest calms him down (7, 63); | 1.5 |
| 6 | battles windmills and ends mauled and on the ground (8, 69–70) | 6.3 |
| 7 | assails two friars who run away from him (8, 74–75) | 1.6 |
| 8 | fights and defeats an armed Biscayan page (8, 76–78 and 9, 83–84) | 8.8 |
| 9 | forbids every one, with his hand on the pommel of his sword, from following Marcela (14, 128) | 0.7 |
| 10 | is beaten by a score of Galician muleteers (15, 132) | 6.9 |
| 11 | is punched, bloodied, and stepped on by the muleteer from Arévalo (16, 146) | 6.6 |
| —61→ | ||
| 12 | is hit on the head with an oil lamp by the innkeeper (16, 151) | 2.4 |
| 13 | watches Sancho's being tossed without being able to defend him other than by yelling (17, 156) | 1 |
| 14 | fights two flocks of sheep and the shepherds stone him with their slings (18, 165–66) | 7.4 |
| 15 | attacks twenty-six unarmed mourners on horseback, breaking the leg of one of them (19, 174) | 6.7 |
| 16 | cannot find the source of some horrible noise because Sancho ties Rocinante's legs (20,181–83) | 1.7 |
| 17 | hits Sancho twice on the back with his lance because he is mocking him (20, 193) | 1.8 |
| 18 | attacks an itinerant barber and seizes the «helmet of Mambrino» (21, 198) | 2 |
| 19 | frees a chain of galley slaves, wounding a commissary and some guards (22, 219) | 7.3 |
| 20 | is stoned by the galley slaves, falls from Rocinante, and he and Sancho are despoiled (22, 221) | 8.4 |
| 21 | falls on his back, hit by Cardenio (24, 245) | 2.9 |
| 22 | asks Andrés to tell the guests about his rescuing him, and Andrés obliges (31, 351–54) | 6 |
| 23 | fights some giants, and is buffeted by the innkeeper for puncturing his wineskins (35, 411–12) | 4.8 |
| 24 | spends the night hanging from a rope tied around his wrist by Maritornes (43–44, 519–22) | 4.5 |
| 25 | causes a free-for-all melee in the inn but retains the «helmet of Mambrino» (44–45, 532–39) | 6.8 |
| 26 | fights the officers of the Santa Hermandad who try to apprehend him (45, 541) | 3.5 |
| 27 | is tied, caged, and set in a cart pulled by oxen (46, 550) | 7.9 |
| 28 | fights with a goatherd (52, 600–01) | 2.2 |
| 29 | attacks some flagellants, one of whom hits him with a wooden fork (52, 603–04) | 7.1 |
| Don Quixote, Part II | ||
| 30 | falls with his horse when a clown scares Rocinante and fails to defend himself (11, 89–92) | 5.4 |
| 31 | fights and defeats the Knight of the Mirrors (14, 106–17) | 9.4 |
| 32 | threatens to kill a cart driver if he does not open the lion cages he is carrying (17, 134) | 1.3 |
| —62→ | ||
| 33 | challenges a lion, who gets up, yawns, and turns his rump at him (17, 134–37) | 1.9 |
| 34 | defends the newly wedded couple when Basilio's stratagem is discovered (21, 173) | 2.6 |
| 35 | destroys Maese Pedro's puppet show defending Don Gaiferos and Melisendra (26, 215) | 0.6 |
| 36 | tries to defend Sancho but flees when his enemies throw stones at him (27, 226–27) | 1.4 |
| 37 | inveighs against the flour millers working at the river Ebro (29, 238) | 1.1 |
| 38 | faces a wild boar (34, 277) 0.8 39 is attacked by two or three cats, one of which scratches his face and bites his nose (46, 359) | 2.1 |
| 40 | is attacked by pinching ghosts (48, 378) | 1.2 |
| 41 | triumphs over Tosilos with some help from Cupid (56, 439–42) | 2.3 |
| 42 | is trampled by a throng of cowboys and bulls (58, 459–61) | 4.6 |
| 43 | tries to whip Sancho but is overpowered by his squire who pins him to the floor (60, 470–71) | 3.6 |
| 44 | is caught unprepared and unarmed by the men of Roque Guinart (60, 472–73) | 0.9 |
| 45 | is defeated by the Knight of the White Moon (64, 510–14) | 10 |
| 46 | is trampled by a drove of swines (68, 532–33); | 4.9 |
| 47 | is taken prisoner and led to the ducal palace (69, 535–42) | 2.5 |
Using the data entered in Table 1, Figure 13 is a two-dimensional trace of Don Quixote's triumphs (white peaks) and defeats (shaded peaks), in phase space17.
—63→Figure 13. A representation of Don Quixote's triumphs and defeats.
The unevenness shown in the trace representing Don Quixote's triumphs and defeats is the result of conditions inherent in all literary works: events do not recur in the same fashion in two different works, events do not share the same nature from work to work, and no two events of the same character are ever identical; hence, the distribution, character, and magnitudes of the disruptions are unique to each work. In the case of Cervantes' work, some of the defeats listed in Table 1 are merely personal disappointments with no serious repercussions (event 1), whereas others are outright, public embarrassments with important lasting effects in the system (45); a victory may be considered, simply, as a personal satisfaction (37), or it may assume the proportions of a legendary feat (6). When Don Quixote is alone, the swing is barely noticeable (1); when there are witnesses to his deeds (4), or when coarse reality and chivalric fantasy mix (42), the swings are ampler; and when two or more triumphs (or defeats) take place immediately one after the other, the iteration or interweaving of the conflicting behaviors makes them resonate, and the magnitude of the swing increases accordingly (11–14). The most memorable adventures of Don Quixote occur in the first half of Part I: the knighting of Alonso Quijana (2), the rescue of Andrés (3), the encounter with the Toledan merchants (4), the finding of Mambrino's helmet (18), and the battles with windmills (6), the Biscayan page (8), muleteers (10 and 11), sheep (14), and galley slaves (20). Starting on Chapter 24 of Part I the system begins to settle into a dynamically stable state, punctured only sporadically by unexpected bursts of energy. The increasing preponderance of the constant over the variables —64→ tally closely with the randomness of the narrative gaps left behind by the substantive authorial changes made to Part I (Figure 3) and the already studied irregular behavior of words with more than one spelling (Figure 6), thus echoing the reducibility that the creative and orthographic processes exhibit throughout the entire system's own time scale.
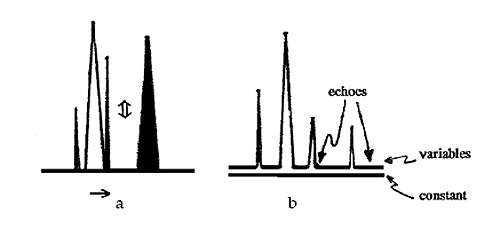
This is, perhaps, the most appropriate place to introduce the concept of «time» in this study. I consider «time» to be the fourth dimension of all written discourse18. In the specific case of Don Quixote, the story flows in one direction (→): Alonso Quijana reads books of chivalry, goes into the world seeking adventures, hovers between past and present in his deeds, and dies. Don Quixote's anachronistic quest and his «living» in sixteenth-century Spain produce, on the other hand, a series of swings going back and forth between present and past, and it may be represented by a double arrow (←→). Don Quixote is, therefore, a word system that functions under two distinct «time arrows», Figure 14a. The beginning and ending of the episodes depicting Don Quixote's triumphs and defeats can be fixed in the text, but the exact places where these events start and end cannot be pinpointed with any accuracy because the generating forces and their echoes prevent the variables from becoming one with the constant throughout most of the system, Figure 14b19.
—65→Figure 14. Quixote's triumphs and defeats, showing the two «time arrows» under which the word system functions (a), and the areas where the echoes of the events resonate (b).
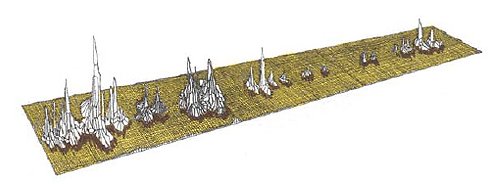
Figure 15 is a representation of four-dimensional Don Quixote (width, length, height, and time; time goes into the back of the page).
Figure 15. Power spectrum for Don Quixote.
The peaks and resonating areas drawn in Figures 13 to 15 are too detailed to offer a visually unobstructed representation of the overall process. An optimate and truer representation of this phenomenon would consist of a continuous, closed trace of the «bases» of the peaks joined to its mirror image at the points in the text where Don Quixote's triumphs and defeats begin (I, 1; 25) and —66→ where Alonso Quijana renounces his chivalric persona (II, 74; page 556, line 39565). The area circumscribed by this trace would be the strange attractor in Don Quixote, Figure 1620.
Figure 16. The strange attractor in Don Quixote.
The strange attractor separates the static, flat, conforming constant (sixteenth-century Spain, Italy, Algiers, the hidalgo Alonso Quijana) from the peaked, non-conforming projections (Don Quixote's triumphs and defeats) that raise over the constant of the system. All points of Don Quixote, all peaks and basins of the system surge from, and converge in, this strange attractor. The chaotic areas of the system are the points on the valley near the boundaries where peaks and basins meet. When, and where, these areas come into contact, the result is unpredictable oscillations that tint the nearby areas with the differing tones of both behaviors. Taking advantage of the edge that humanities have over science, let us now draw the contained system that is Don Quixote as a four-dimensional literary phenomenon made out of hundreds of thousands of words, Figure 17.
Figure 17. Don Quixote.
—67→
One should not be misled by the apparent simplicity of the
portraits drawn in Figures 15, 16, and 17. As Allan McRobie and
Michael Thompson note, «attractors generally evolve smoothly,
but at certain critical points, called bifurcations, the attractor may
split into different attractors or may simply disappear»
(155). And
this is exactly what happens in Don Quixote, where the main
attractor splits into different attractors for, amongst others, «The
Captive's Tale» (I, 39–42) and the episodes dealing with Sancho's
ínsula (II, 45, 47, 49, 51, and 53) and temporarily disappears «under»
the short story of «El curioso impertinente» in two occasions (I, 33,
lines 12068–13681 and 35, lines 13840–14022), reappearing for Don
Quixote's battle with the wineskins (lines 13682–839) and at the
conclusion of the interpolated story (line 14022); but each secondary
attractor requires a separate study on its own.
To conclude, chaos theory is, intrinsically, a scientific endeavor designed to explain the workings of a Universe created by God. When dealing with the artificial worlds created by us, the thrust of chaos theory should be aimed at representing the universal essence of these worlds. Thus, my purpose for studying Don Quixote from a chaological point of view was not to explain this work of Cervantes or to elucidate aspects pertaining to literary theory, nor, as is the case in instances of natural phenomena, to predict the future behavior of the system or to induce the phenomenon into behaving differently by altering initial conditions. My aim was, simply, to give texture and physical entity to the spirit of Cervantes' work.
The drawings included in this study are not computer generated, but I regard them, nevertheless, as the most important elements of my work because they make my findings and conclusions visually accessible to the imagination. I think that an image similar to the one drawn in Figure 17 can be arrived at by following and elaborating on Percival's «recipe» for producing orbits of dynamic systems (262–66, and Figures 14.6–14.29). I lack the necessary computer expertise to follow up and carry out Percival's detailed instructions in practice but, who can tell? Some day we may, after all, be able to devise an elegant mathematical formula based on the text of this work of Cervantes' for a computer to plot and project on the screen many other multicolored portraits of Don Quixote. —68→ Only then and thus may scientists be able to recognize the numerical validity and perceive the beauty of the things imagined by humanists.
A literary work is not simply what is written, nor just what we
read or hear, nor solely the many things it «says» to us. The ineffability
in Don Quixote is an essence inherent in all literary works; an
essence shared by all other works created by us. It is a fleeting
image, an indescribable vision one must capture and record visually.
«Chaos is exciting because it opens up the possibility of simplifying
complicated phenomena»
, states Stewart, «Chaos is fascinating
because of its interplay of mathematics, science, and technology.
But above all chaos is beautiful»
(«Portraits», 44). This
study and my conclusions are yet another step towards a humanistic
appreciation of Stewart's glowing evaluation of chaos. It is an
attempt to find out what Cervantes and scientists have been up to,
and then feed the answers through my own sensibilities.
The Barber
—70→Briggs, John, and F. David Peat. Turbulent Mirror. New York: Harper & Row, 1989.
Cervantes, Miguel de. Don Quixote de la Mancha: An Old-Spelling Control Edition Based on the First Editions of Parts I and II. Ed. R. M. Flores. 2 vols. Vancouver: British Columbia UP, 1988.
Clark, John W. «Views from the Ivory Tower's Basement. A Commentary on 'The Clock and the Cloud: Chaos and Order in El diablo mundo'». Revista de Estudios Hispánicos 26 (1992): 226–50.
Flores, R. M. «Cervantes at Work: The Writing of Don Quixote, Part I». Journal of Hispanic Philology 3 (1979): 135–60.
——. The Compositors of the First and Second Madrid Editions of Don Quixote Part I. London: Modern Humanities Research Association, 1975.
——. «The Compositors of the First Edition of Don Quixote, Part II». Journal of Hispanic Philology 6 (1981): 3–44.
——. «¿Qué hay en los apellidos Quijada, Quesada y Quijana? Fuentes históricas, teoría narratológica y bibliografía analítica en la crítica literaria». Bulletin Hispanique 99 (1997): 409–22.
Gleick, James. Chaos: Making a New Science. New York: Viking, 1987.
McRobie, Allan, and Michael Thompson. «Chaos, Catastrophes, and Engineering». Exploring Chaos: A Guide to the New Science of Disorder. New York: Norton, 1993. 149–61.
Peitgen, Heinz-Otto, and Peter H. Richter. The Beauty of Fractals: Images of Complex Dynamical Systems. Berlin: Springer, 1986.
Percival, Ian. «Chaos: A Science for the Real World». Exploring Chaos: A Guide to the New Science of Disorder. New York: Norton, 1993. 11–21.
Pickover, Clifford A. Computers, Pattern, Chaos and Beauty: Graphics from an Unseen World. New York: St. Martin's P, 1990.
Stewart, Ian. Does God Play Dice? The Mathematics of Chaos. London: Blackwell, 1989.
——. «Portraits of Chaos». Exploring Chaos: A Guide to the New Science of Disorder. New York: Norton, 1993. 44–58.